红黑树和平衡二叉树的优缺点,红黑树为什么是平衡二叉树

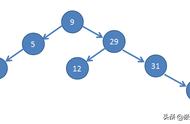
情况3：要删除的是节点 a，它有两个非空子节点，并且节点 a 的后继节点不是a的右子节点：

1. 找到后继节点 d，并将它删除，删除后继节点 d 的过程参照 CASE 1。
2. 用d来替换a，并且d的颜色设置的跟a颜色一样。
3. 如果节点 d 是黑色，为了不违反红黑树路径相同原则，给节点 d 的右子节点 c 多加一个黑色，这个时候节点 c 就成了红 - 黑或者黑 - 黑。
4. 此时关注节点变成了节点 c，第二步的调整操作就会针对关注节点来做。

经过初步调整之后，关注节点变成了红 - 黑或者黑 - 黑 节点。针对这个关注节点，再分四种情况来进行二次调整。二次调整是为了让红黑树中不存在相邻的红色节点。

情况1：关注节点是 a，它的兄弟节点 c 是红色的，我们就依次进行下面的操作：

1. 围绕关注节点 a 的父节点 b 左旋。
2. 关注节点 a 的父节点 b 和祖父节点 c 交换颜色。
3. 关注节点不变，继续从四种情况中选择适合的规则来调整。

情况2：关注节点是 a，它的兄弟节点 c 是黑色，并且节点 c 的左右子节点 d、e 都是黑色：

1. 将关注节点 a 的兄弟节点 c 的颜色变成红色，因为接下来黑圆圈会上移，那么c比a多个深色。
2. 从关注节点 a 中去掉一个黑色，此时节点 a 就是单纯的红色或者黑色。
3. 给关注节点 a 的父节点 b 添加一个黑色，这个时候节点 b 就变成红 - 黑或者黑 - 黑
4. 关注节点从 a 变成其父节点 b，继续从四种情况中选择符合的规则来调整。

情况3：关注节点是 a，它的兄弟节点 c 是黑色，c 的左子节点 d 是红色，c 的右子节点 e 是黑色：

1. 围绕关注节点 a 的兄弟节点 c 右旋。
2. 节点 c 和节点 d 交换颜色。
3. 关注节点不变，跳转到情况4，继续调整。