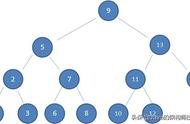
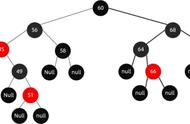
由于是从13节点出现的不平衡,因此对13节点进行右旋,得到结果:

而后再对其节点进行变色,得到结果:

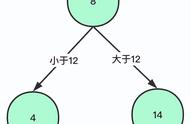
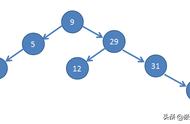
折半查找法要求的是一个有序的序列,红黑树对应的也是一个有序的、平衡的序列:
template<typename T> struct TreeNode { T data; int balance; //左子树深度 - 右子树深度 TreeNode *parent; TreeNode *LeftChild; TreeNode *RightChild; }; bool FindElem(TreeNode * node,ElemType elem) { if(node != NULL) { if(node->data == elem)//找到元素 return true; else if(node->data > elem)//只需继续查找左子树 return FindElem(node->LeftChild, elem); else if(node->data < elem)//只需继续查找右子树 return FindElem(node->RightChild, elem); } else return false; }
每次添加/删除一个元素后,势必会影响到某处的深度,就有可能使得操作之后的二叉树不再处于平衡状态。把不平衡的地方进行某种所谓的“旋转”使得重新变成平衡的状态。
红黑树的用途有很多,例如STL的关联容器的底层数据结构就是黑红树:

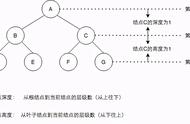
是为每个节点添加了一个字段int balance。
balance = 左子树深度 - 右子树深度
(两个数相减的值可以作为这两个数的一种比较)
1)当balance的绝对值<=1的时候就认为“差距不大”,为“平衡状态”;
2)当balance的绝对值>=2的时候就认为“差距过大”,为“不平衡状态”;
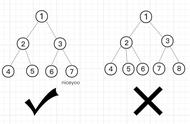
3)定义二叉平衡树:所有节点的balance的绝对值均<=1;
每次添加/删除一个元素,势必会影响到某处的深度,进而影响到balance的值,就有可能使得操作之后的二叉树不再处于平衡状态。
解决办法就是:
每次添加/删除一个元素后,根据balance的变化,把不平衡的地方进行某种所谓的“旋转”使得重新变成平衡的状态。
每次的添加/删除操作都是针对一个平衡的二叉树,如果操作完成后不平衡了则重新整理成平衡状态,这就保证了二叉树时刻处于平衡状态。
对于一棵已经处于平衡状态的二叉树,添加/删除一个元素对其的平衡状态的影响实际上非常有限。
由于原先的balance只有三个值“0,1,-1”,所以一个元素的影响只有使得“-1变成-2”或“1变成2”才可以破坏平衡。
旋转操作代码:
void Swing(TreeNode<ElemType>*p) { if (p->balance == 2) //balance=左子树深度 - 右子树深度 { if (p->LeftChild->balance == 1)//LL型旋转 SwingLL(p, p->LeftChild); else if (p->LeftChild->balance == -1)//LR型旋转 SwingLR(p, p->LeftChild, p->LeftChild->RightChild); } else if (p->balance == -2) { if (p->RightChild->balance == -1)//RR型旋转 SwingRR(p, p->RightChild); else if (p->RightChild->balance == 1)//RL型旋转 SwingRL(p, p->RightChild, p->RightChild->LeftChild); } } void SwingLL(TreeNode<ElemType>*A, Tree Node<ElemType>*B) { TreeNode<ElemType> *parent = A->parent; if (parent != NULL) { if (IsLeftChild(A)) parent->LeftChild = B; else parent->RightChild = B; } else root = B; A->LeftChild = B->RightChild; if (B->RightChild != NULL)B->RightChild->parent = A; B->RightChild = A; A->parent = B; B->parent = parent; A->balance = 0; B->balance = 0; } void SwingLR(TreeNode<ElemType>*A, TreeNode<ElemType>*B, TreeNode<ElemType>*C) { A->LeftChild = C; C->parent = A; B->RightChild = C->LeftChild; if (C->LeftChild != NULL) C->LeftChild->parent = B; C->LeftChild = B; B->parent = C; TreeNode<ElemType> *parent = A->parent; if (parent != NULL) { if (IsLeftChild(A)) parent->LeftChild = C; else parent->RightChild = C; } else root = C; A->LeftChild = C->RightChild; if (C->RightChild != NULL) C->RightChild->parent = A; C->RightChild = A; A->parent = C; C->parent = parent; if (C->balance == 1) { C->balance = 0; B->balance = 0; A->balance = -1; } else { C->balance = 0; B->balance = 1; A->balance = 0; } }
-End-
,