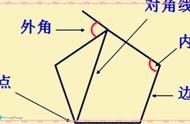
我们知道,n边形的内角和是(n-2)×180°,而外角和是360°.由此可见,多边形的内角和与边数n有关,而外角和却与边数n无关,是一个常数.因此,利用多边形内角与相邻的外角互补这一关系,将多边形内角问题转化为外角问题,可以起到以不变应万变之效果,其解法特别巧妙.请看:
例1 一个多边形的每个内角都等于144°,则它的边数是______.
分析与解:一般解法是:设边数为x,则由内角和公式,得(x-2)×180°=x×144°,解之,得x=10.这是直接从题意入手,通过设元,然后运用内角和公式列方程.其解法当然是无可非议的.但是,若从外角入手,则易知每个外角为180°-144°=36°,又因为外角和为360°,因此,共有360°÷36°=10(个)外角,从而可知所求的边数为10.
例2 凸n边形恰好有三个内角是钝角,这样的多边形边数n的最大值是( )
A.4 B.5 C.6 D.7
分析与解:若直接考虑内角"只有三个钝角",则显然是无从下手的.从外角入手,因为n个内角中恰有3个钝角,所以在n个外角中恰好有3个锐角,其余(n-3)个外角是直角或钝角,由外角和等于360°可知这(n-3)个外角中最多只能有3个直角(或钝角),因此,n-3≤3,n≤6,所以n的最大值为6,选C.
例3 凸2019边形的内角中,非锐角的个数至少有______个.
分析与解:设凸2019边形的内角中,非锐角的个数有n个,则锐角的个数为(2019-n)个,与这(2019-n)个内角相邻的(2019-n)个外角都为钝角或直角,而(2019-n)个外角中最多有3个直角(或钝角),所以2019-n≤3,解得n≥2016,故n的最小值为2016,因此,凸2019边形的内角中,非锐角的个数至少有2016个.
例4 已知n边形的每个内角都是10°的整数倍,其中三个内角分别是60°、90°和120°,其余各内角的度数都相等,求n的所有可能值.
分析与解:由已知,三个外角分别为120°、90°和60°,所以余下的(n-3)个外角的和为360°-(120° 90° 60°)=90°.又因为这(n-3)个内角的度数是10°的整数倍,所以这些内角的外角也是10°的整数倍.设这些外角每个的度数为m·10°(m为正整数),则(n-3)m·10°=90°,m=9/(n-3),
因为n是大于3的整数,所以n=4,6,9,12.此即n的所有可能值.
例5 若凸n边形的每个内角都是30°的正整数倍,则n的最小值与最大值之和是____.
分析:设一个内角为α,其外角为β,则β=180°-α,因为α是30°的整数倍,所以β也是30°的整数倍,所以外角β的最小值为30°,最大值为150°,故360/150≤n≤360/30,即2.4≤n≤12,因为n为整数,所以n的最小值为3,最大值为12,因此,n的最小值与最大值的和为15.
例6 定义:若凸n边形的n条边相等,n个内角相等,这样的n形叫做正n边形.若正n边形的内角度数是整数,这样的n有______个.
分析与解:因为内角是整数,所以外角也是整数,而每个外角的度数为360/n,所以360/n是整数,因此,问题在于确定360的正整数因数的个数.
由于360=2^3×3^2×5,所以,360的正因数个数共有(3 1)(2 1)(1 1)=24个(包括1),而n>2,去掉1和2两个因数,故n的值共有22个.
评注:求一个正整数N所有约数个数(包括1)的方法是:将这个整数N分解成质因数的积a1^p1·a2^p2·…·ak^pk,则N的所有约数的个数为(p1 1)(p2 1)…(pk 1).
,