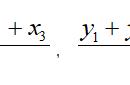南宋数学家秦九韶(约1202~1261)的著作《数书九章》第三章田域类有一道题目(沙田求积):
问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里。里法三百步,欲知为田几何?
秦九韶独创三斜求积术,解决了这类已知不等边三角形的三边边长,求面积的问题。
解决此类问题,西方数学家常用海伦(约公元50年)公式,中国独创秦九韶公式。这两种公式是等价的。
解这个题目还有一种方法,即求高法。
三斜求积术用公式法可以直接把数据代入公式,计算出三角形的面积。用求高法是以一条边为底边,从对角顶点向底边作垂线,把任意三角形划分为两个直角三角形,再求高即得三角形的面积。
先讨论用三斜求积术如何解决问题。
已知任意三角形的三边边长,把数据代入公式,就求出面积。这就是南宋数学家秦九韶创造的三斜求积术。
《数书九章》给出的答案和解法如下:
答曰:田积三百一十五顷。
术曰:以少广求之。以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上。以小斜幂乘大斜幂,减上,余四约之,为实。一为从隅,开平方,得积。
看不懂术文?那就请看用现代数学符号改写成的秦九韶公式,如下图所示:

秦九韶的三斜求积术给出了一般的计算公式,是对几何学的一大贡献。但由于诸多原因,秦九韶的原始证明已经失传。如何根据中国几何的特色补出秦九韶公式的证明,是众多学者研究探讨的热点。
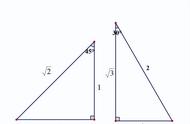
著名数学家吴文俊(1919~2017)在《出入相补原理》一文中,给出了一个漂亮的补证。在欣赏吴文俊的证明之前先介绍《九章算术》中研究直角三角形的一个成果。吴文俊先生以古人的研究成果为引理,巧妙地推导出秦九韶公式,古韵古风,简朴自然。
《九章算术》有这样一道勾股定理的简单应用题:

折竹求高
今有竹高一丈,末折抵地,去本三尺。问折者高几何?
答曰:四尺二十分尺之十一。
答案是怎样计算出来的呢?请看下图:

为了解决上面提出的折竹求高的问题,古人推导出一个常用的公式,推导过程请看下图,结论就是公式(4)。