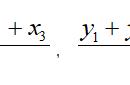刘徽根据出入相补原理用几何方法推导出公式(4)
把题目数据代入公式(4)计算,就得到答案4又20分之11(单位:尺)。
吴文俊先生作出的补证抄录如下:
沙田求积:已知三边求面积。
现成的解题工具盘点:(1)三角形面积公式:S=½ahₐ;(《九章算术》有此公式)
(2)勾股定理:a² b²=c²;(赵爽和刘徽已证明)(3)勾股公式:已知勾,已知股弦和,可求股。(刘徽注解《九章算术》推导出此公式)
解题计划:
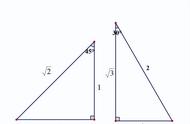
(1)以大斜为底边作图并标注斜三角形;
(2)作高构造勾股形并标注;
(3)以大斜的两段构造辅助元素勾股形并标注;
(4)用勾股定理求勾;
(5)用勾股公式求股;
(6)已知股和小斜,可用勾股定理求高;
(7)已知高和大斜,可用三角形面积公式求面积;
(8)提炼出秦九韶公式,所有辅助元素可以在过程中出现,不允许在结论中出现。公式中只能有三斜和常数。
解题过程:
勾方=(中²-高²)-(小²-高²)
=中²-小²=14²-13²=196-169=27
股=(股弦和方-勾方)÷2倍股弦和=(15²-27)÷(2×15) (折竹求高的公式4)
=(225-27)÷30=198÷30=6.6
高方=小方-股方=13²-6.6²
=169-43.56=125.44
高=11.2

笔算开平方图一
面积=½大斜×高=15×11.2÷2=84
提炼公式
公式验证:

秦九韶公式
把a=13,b=14,c=15代入公式
a²c²=169×225=38025
a² c²-b²=169 225-196=198
½(a² c²-b²)=99
½²(a² c²-b²)²=99²=9801
a²c²-½²(a² c²-b²)²=38025-9801=28224
28224开平方=168

笔算开平方图二
面积=168÷2=84
怎样从以上解法概括出具有一般化和普遍性的秦九韶公式?
请看下图: