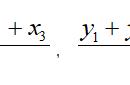等边三角形的高怎么求出来的（知道等边三角形的三边怎么求高） - 原点资讯

沙田求积

由勾股定理可得:

AD²=AB²-x²=13²-x²

AD²=AC²-(15-x)²=14²-(15²-30x x²)

由以上两式可得

13²-x²=14²-(15²-30x x²)

去括号

13²-x²=14²-15² 30x-x²

整理化简

30x=225 169-196

解之得

x=6.6

由勾股定理可得

高²=AD²=13²-6.6²

高=11.2

苏联科普作家别莱利曼的解法如下:

BD²=13²-AD² ,

BD²=14²-DC²,

从上列二式得：

13²- AD²=14²-DC²,

DC² - AD² =14²-13²=27。

但是

DC² - AD²=( DC AD )( DC - AD )

=15( DC - AD )。

因此

15( DC - AD )=27,

DC - AD =27÷15=1.8。

由 DC - AD =1.8,

DC AD =15,

得：2DC=16.8,

就是 DC=8.4。

现在就不难算出三角形的高来：

AD =√(14²-8.4²)=11.2

以上解法其实相当于解用勾股定理列出的二元二次方程组:(请看下图)

等边三角形的高怎么求出来的,知道等边三角形的三边怎么求高(17)

破解美国竞赛题

我们掌握了求高法，现在做两道习题来巩固一下。首先，我们来破解一道美国竞赛题，请看下图。

等边三角形的高怎么求出来的,知道等边三角形的三边怎么求高(18)

容易想到从上底的两个端点向下底作垂线，把梯形分为两个直角三角形和一个矩形，分别计算面积再求和。

一眼看出两个直角三角形可以拼成三斜为8，10，12的不等边三角形，求出它的高，就可以用梯形面积公式计算得到问题的答案。

但是，很遗憾，(8，10，12)不是海伦数组，所以三角形以及梯形面积都是无理数。

什么是海伦数组？秦九韶的三角形三斜都是整数，面积也是整数，就称为海伦三角形。海伦三角形的三边边长就称为海伦数组，例如(13，14，15)。海伦数组包含毕达哥拉斯三元数组(勾股数组)。

我们来修改一下题目数据。怎么修改？就是构造一个海伦三角形。直角三角形的三边如果是勾股数组，那么就称为勾股形。我们可以用两个适当的勾股形来拼成一个海伦三角形。

举个例子，(6，8，10)和(8，15，17)都是勾股数组，而且有相等的直角边，所以可以拼成海伦三角形。

因为构造出的海伦数组是(10，17，21)，所以把梯形的左腰数据改成17，右腰数据改成10，下底数据改成31。这样修改后，答案就是整数了。

辅助线的做法还可以过上底的左端点作右腰的平行线，或者是过上底的右端点作左腰的平行线。

这种作法就把梯形分为海伦三角形和平行四边形，求高后就得到梯形的面积。

现在问题转化为如何求海伦三角形(10，17，21)的高。

既然提到了转化，请允许我先讲个关于转化的笑话，如何再继续解题。

中场休息脱口秀

噢，我倒了！

先说一个关于数学家的笑话。这个笑话不是我说的，但我也不知道是谁说的。准备，开始：

在一次心理学实验中，一位数学家被安排在一个房间里，房间里有水池、烧水壶和火炉。数学家被要求烧一壶水。他拿起空水壶，在水池里接满水，放到火炉上，把火打开。然后他进入另一个房间，房间里有水池、装满水的水壶和火炉。他再次被要求烧一壶水。他拿起水壶，将水倒进水池里，然后宣布：“我已经将这个问题转化为了之前已经解决的问题。”

虽然数学家的行为很蠢，这个笑话还是突出了一个重点。它告诉我们解决问题——不仅是数学问题，也包括我们想解决的任何问题——的方法有两种：

1.直接解决问题。

2.解决一小部分问题，然后发现余下的问题类似于某个答案已知的问题。然后照做。

换句话说，问题只有在我们不知道如何解决时才难。一旦我们知道如何做了，我们就可以开启自动驾驶模式，然后坐等问题解决。比如，假设我们在某个不熟悉的地方迷路了，想要回家。怎么才能回家呢？通常你不会突然被绊倒摔进你家后院，然后说：“噢，到家了。”也就是说，你无法一下解决迷路的问题。更有可能的是你遇到某个你熟悉的地方。你说：“噢！那是美沙酮门诊，窗户玻璃是彩色的！我知道从这里怎样去我奶奶家。”到达一个熟悉的地方后，你就能将问题转化为你以前解决过的问题，剩下的事情就简单了。数学就是这样！要深刻理解这一点，最好的方式之一就是发明微积分。现在我们就来尝试一下。