【套路秘籍】---千里之行始于足下
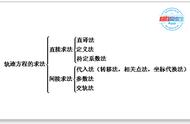
求轨迹方程的常用方法:
⒈直接法:直接将条件翻译成等式,整理化简后即得动点的轨迹方程,这种求轨迹方程的方法通常叫做直接法。
⒉定义法:如果能够确定动点的轨迹满足某种已知曲线的定义,则可利用曲线的定义写出方程,这种求轨迹方程的方法叫做定义法。
⒊相关点法:用动点M的坐标x,y表示相关点P的坐标(Xo、Yo),然后代入点P的坐标(Xo、Yo)所满足的曲线方程,整理化简便得到动点Q轨迹方程,这种求轨迹方程的方法叫做相关点法。(用未知表示已知,带入已知求未知)
⒋参数法:当动点坐标x、y之间的直接关系难以找到时,往往先寻找x、y与某一变数t的关系,得再消去参变数t,得到方程,即为动点的轨迹方程,这种求轨迹方程的方法叫做参数法。
⒌交轨法:将两动曲线方程中的参数消去,得到不含参数的方程,即为两动曲线交点的轨迹方程,这种求轨迹方程的方法叫做交轨法。
【修炼套路】---为君聊赋《今日诗》,努力请从今日始