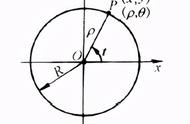
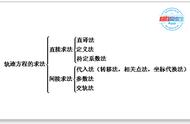
【题型一】 直接法求轨迹1
解题步骤:
1.根据已知条件及一些基本公式(两点间距离公式、点到直线的距离公式、直线斜率公式等)
2.根据公式直接列出动点满足的等量关系式,从而得到轨迹方程;
3.注意“多点”和“少点”,一般情况下,斜率和三角形顶点等约束条件.
【题型二】 相关点代入法求轨迹2
一般情况下,所求点的运动,依赖于另外一个或者两个多个点的运动,可以通过对这些点设坐标来寻求代换关系.
1、求谁设谁,设所求点坐标为(x,y);
2、所依赖的点称之为“参数点”,
3、“参数点”满足某个(些)方程,可供代入;
4、寻找所求点与“参数点”之间的坐标关系,反解参数值;
5、代入方程,消去参数值.
【题型三】 定义法求轨迹4
若动点轨迹的条件符合某一基本轨迹的定义,就用定义直接求.
1.椭圆,双曲线,抛物线的定义;
2.一些特殊图像
定义,如阿波罗尼斯圆;
3.两个圆内外切情况下,较多与圆锥曲线定义有关.
【题型四】 交轨法求轨迹5
交轨法,即轨迹交点法
1.所求点满足条件方程1
2.所求点满足条件方程2
3.动点是两轨迹方程,则满足两个轨迹所组成的方程组,通过两个方程选择适当的技巧消去参数得到轨迹的普通方程
4.参数法求轨迹方程,关键有两点:一是选参,容易表示出动点;二是消参,消参的途径灵活多变.
【题型五】 参数求轨迹6
解题步骤:
1 引入参数,用此参数分别表示动点的横纵坐标
2.消去参数,得到关于方程,即为所求轨迹方程.
【题型六】 立体几何中的轨迹8
立体几何内的轨迹,尝尝从以下方向切入
1.建系,利用空间坐标系求出方程;
2.通过转化,把空间关系转化为平面关系,把空间轨迹转化为平面轨迹求解.
【题型七】 向量与求轨迹12
【题型八】 新高考:复数中求轨迹17