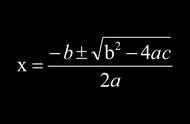一、引入
对于一元二次方程的一般形式ax² bx c=0(a≠0),我们尝试采用配方法求解:


二、公式法及其两个用途
通过上面解一元二次方程的一般式ax² bx c=0(a≠0),当b²-4ac≥0时,方程有解,那么解出来的根一定是:

这个叫做求根公式
我们发现,任何一个一元二次方程的根只和系数a,b,c有关,也就是说只要确定了系数,就可以得到方程的根,这就是公式法的第一个用途——根据系数直接确定方程的根
另外我们发现:
当b²-4ac>0时,方程有两个不等实根
当b²-4ac=0时,方程有两个相等实根
当b²-4ac<0时,方程无实根
我们经常把△=b²-4ac叫做根的判别式(△是希腊字母,读作“德尔塔 Delte”),利用它我们可以判别一元二次方程根的个数,这也是公式法的第二个用途。
三、利用公式法求解的一般步骤


【公式法法求解的一般步骤】:
①将方程化为一般形式
②确定a,b,c的值
③判断△=b²-4ac的符号
④当b²-4ac≥0时(有实根),我们将a,b,c代入
得到方程的两个根
当b²-4ac<0时(无实根),我们直接判定方程无实根
【理解】
1、在利用(代入)求根公式之前,要有两个准备工作:
一是必须先把方程化为一般式,因为只有这样才能确定a,b,c
二是判定△=b²-4ac的符号,当△≥0时才能代入求根公式,而当△<0时,直接得到方程无实根即可
2、由于在判断△符号的过程中,已经把△的值求出,所以在后续的求解中,直接代入即可。另外当△=0时,求根公式中的根号部分为0,此时直接代入x=-b/2a即可
3、我们发现,对于一元二次方程ax² bx c=0(a≠0),当a、c异号时即ac<0时,△=b²-4ac中b²≥0,-4ac>0,所以此时一定有△>0,即方程有两个不等实根,如例题中的方程5x²-4x-1=0,由于a、c异号所以方程必然有两个不等实根,这在做小题时,是个不错的技巧。
四、练习题
1、用公式法解方程:
(1)x² 3x-4=0
(2)x²-2x 5=2x 4
2、填空
(1)快速判断:方程x²-4x-1=0_______实数根(填"有两个不等"、"有两个相等"或"无")
(2)已知关于x的一元二次方程x²-kx 4=0有两个相等的实数根,则k=_____
(3)若关于 x的一元二次方程2x²-2x (a 1)=0没有实数根,则整数a的最小值为__________.
【参考答案】
1、(1)x=1或-4(2)x=2±√3
2、(1)两个不等;(2)k=±4;(3)0
,