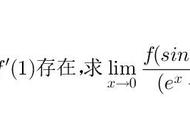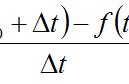导数是微积分学中最重要的概念之一,它描述了函数在某一点处的变化率。导数的定义可以追溯到17世纪,由法国数学家莱布尼茨提出。在微积分学中,导数表示函数在某一点处的变化率,即函数在该点处的斜率。
导数的定义可以表述为:若函数y=f(x)在点x0处可导,则称f'(x0)为函数y=f(x)在x0处的导数。导数的几何意义是:函数在某一点处的导数等于该函数曲线在该点处的切线的斜率。

导数的定义
常用的导数口诀包括:
1. 常数函数的导数为零:f'(x)=0,当f(x)=c(c为常数)时,有f'(x)=0。这是因为常数的斜率为零。
2. 常数倍数的函数可导:如果f(x)可导,那么cf(x)也可导,即常数倍数的函数可导。
3. 线性函数的导数是常数:如果f(x)=kx b(k为常数),那么f'(x)=k。这是因为线性函数的斜率是常数。
4. 幂函数的导数可以求出:如果f(x)=x^n(n为整数),那么f'(x)=nx^(n-1)。这是因为幂函数的导数等于原函数乘以指数函数的导数。
5. 三角函数的导数可以求出:sinx的导数为cosx,cosx的导数为-sinx。这是因为三角函数的导数等于原函数乘以指数函数的导数。
6. 反三角函数的导数可以求出:反正弦函数arcsinx的导数为1/√(1-x^2),反余弦函数arccosx的导数为-1/√(1-x^2)。这是因为反三角函数的导数等于原函数乘以指数函数的导数。
7. 对数函数的导数可以求出:如果f(x)=log(a)x(a为正实数),那么f'(x)=1/x*lna。
这是因为对数函数的导数等于原函数乘以指数函数的导数。
8. 复合函数的导数可以求出:如果f(x)=f[g(x)],那么f'(x)=f'[g(x)]*g'(x)。这是因为复合函数的导数等于原函数和内函数的导数的乘积。
9. 隐函数的导数可以求出:如果f(x,y)=0(其中y为x的函数),那么可以通过求解方程来求得y'(x)。这是因为隐函数的导数等于将y作为自变量,其余变量作为常量的函数的导数。
10. 高阶导数的求法:高阶导数的求法是通过对原函数进行求导,直到得到一个n阶导数为止,然后将得到的n个导数相乘得到n阶乘积。例如,一个函数f(x)的二阶导数是f'(x)*f'(x),三阶导数是f'(x)*f'(x)*f'(x),以此类推。
口诀:常为零,指不变,幂降次,正变余,余变正,切割方,割乘切,反分式
以上是常用的导数口诀,可以帮助初学者更好地理解导数的概念和应用。同时,需要注意的是,在实际应用中,需要根据具体问题选择合适的导数定义和口诀来解决问题。