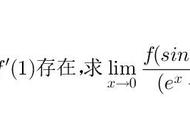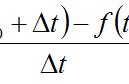导数是微积分中的重要概念之一,它在数学和物理学等领域中有着广泛的应用。本文将从导数的定义、性质和计算方法等方面进行详细介绍,希望能够帮助读者更好地理解和应用导数。
一、导数的定义
导数是函数在某一点处的变化率,可以理解为函数在该点附近的斜率。对于函数y=f(x),在点x处的导数表示为f’(x),也可以写作dy/dx。导数的定义可以用极限来表达,即:
f’(x) = lim (h->0) [f(x h) - f(x)] / h
其中,h表示自变量x的增量。这个定义表明,导数是函数在某一点的极限斜率。
二、导数的性质
导数具有一些重要的性质,下面我们逐一介绍。
可加性:若函数f(x)和g(x)都在点x处可导,则它们的和f(x) g(x)也在该点可导,且导数满足导数的加法法则,即(f g)’(x) = f’(x) g’(x)。
可乘性:若函数f(x)和g(x)都在点x处可导,则它们的乘积f(x)g(x)也在该点可导,且导数满足导数的乘法法则,即(fg)’(x) = f’(x)g(x) f(x)g’(x)。
常数倍数:若函数f(x)在点x处可导,则常数k与函数f(x)的乘积kf(x)也在该点可导,且导数满足常数倍数的法则,即(kf)’(x) = kf’(x)。
复合函数:若函数y=f(u)和u=g(x)都在点x处可导,则复合函数y=f(g(x))也在该点可导,且导数满足复合函数的法则,即(dy/dx) = (dy/du)(du/dx)。
三、导数的计算方法
导数的计算方法主要有以下几种常见的情况:
常数函数的导数为0,即对于常数c,有d/dx© = 0。
幂函数的导数可以通过幂函数的求导法则来计算。对于幂函数y=xn,其中n为常数,有d/dx(xn) = nx^(n-1)。
指数函数和对数函数的导数可以通过指数函数和对数函数的求导法则来计算。对于指数函数y=ax,其中a为常数且a>0且a≠1,有d/dx(ax) = a^x * ln(a)。对于自然对数函数y=ln(x),有d/dx(ln(x)) = 1/x。
三角函数和反三角函数的导数可以通过三角函数和反三角函数的求导法则来计算。例如,对于正弦函数y=sin(x),有d/dx(sin(x)) = cos(x)。对于反正弦函数y=arcsin(x),有d/dx(arcsin(x)) = 1/√(1-x^2)。
四、导数的应用
导数在数学和物理学等领域中有着广泛的应用。下面我们简要介绍一些常见的应用。
切线和法线:导数可以用来求函数曲线上某一点的切线和法线。切线的斜率等于函数在该点的导数,法线的斜率等于切线斜率的负倒数。
极值点:函数在极值点处的导数为0或不存在。通过求导数,可以找到函数的极大值和极小值点。
函数的增减性和凹凸性:函数在某一区间上递增或递减的条件是函数在该区间上的导数大于0或小于0。函数的凹凸性可以通过导数的二阶导数来判断。
泰勒展开:泰勒展开是一种将函数表示为无穷级数的方法,通过导数可以计算函数在某一点的泰勒展开式。
五、总结
导数是微积分中的重要概念,它描述了函数在某一点的变化率。导数具有可加性、可乘性、常数倍数和复合函数等性质,可以通过常见的计算方法进行求导。导数在切线和法线、极值点、函数的增减性和凹凸性以及泰勒展开等方面具有广泛的应用。
希望通过本文的介绍,读者对导数的概念、性质和计算方法有了更深入的理解。在实际应用中,导数是解决问题的重要工具,对于进一步学习和应用微积分具有重要意义。
,