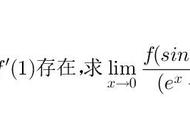荐读:衡水中学疫情期间作息时间表曝光!惊醒无数沉睡中的孩子……助力高考,献给高三党复习大全高中数学优秀视频全集(有更新)最新高三模拟大全(更新)

先简短地回答下我对“什么是导数”的认识:导数是用来找到“线性近似”的数学工具。
下面我来解释一下,为什么我是这样认为的。
在我学习微积分的过程中,我对导数的认知经历了三次变化:
- 导数是变化率、是切线的斜率、是速度、是加速度
- 导数是用来找到“线性近似”的数学工具
- 导数是线性变换
我认为第一种认知比较片面,在多元函数的情况下甚至是错误的。第二种认知更接近微积分的本质,第三种认知是为了实现第二种认知发展出来的。
因为种种原因,我们的学习都是从第一种认知开始的。我会在本文分别介绍一下这三种认知。最后会通过第三种认知回答“多元微积分中,可微函数的切线为什么会共面(此平面即切平面)?”
1 导数是变化率、是切线的斜率、是速度、是加速度
微积分的发明人之一是牛顿,牛顿主要还是研究物理为主,微积分不过是他发明出来研究物理的一个数学工具(大师就是这么厉害)。
因为牛顿研究物理的缘故,所以牛顿用变化率的方式引入了导数(牛顿称之为“流数”)。
在物理里面变化率还是很自然的概念,比如为了求瞬时速度: