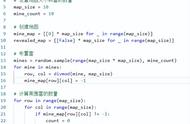
121 情形下,由于左侧 1 的限制,在黄色区域内只能有一格雷,但是中间的 2 至少要求 2 格雷,所以粉色的那颗一定是雷。同理证明另外一侧

1221 情形下,和上面证明过程相同,由于 1 的限制导致在黄色区域内只能有 1 格雷,所以另一个 2 正对的方格一定是雷。
「小编小编,我有个问题,那 121221 呢?按照秘籍填雷的话中间那个 1 附近有两颗雷诶?」

似乎有问题的秘籍?
「这种情况是不可能的!左边数起三个 1 已经覆盖了上面的所有未知空格,所以地雷数至多只有 3 个。但下方显示地雷数为 1 2 2 1 2 1,在只有中间 5 个格子重复计数的情况下都到了 7,大于 3 的 2 倍。所以这种图形是不可能存在的!」
咳咳,把思路收回来,如上所述,扫雷确实是有一些套路的。每日熟读此扫雷秘籍,假以时日,扫雷技艺必将大成。
扫雷还是运气活
Lucky or not,it's a question
虽然人生已经如此地艰难,但我还是要无情地拆穿这一点。想必你此时已经熟练掌握了扫雷的套路,不过在有些时候你还是要面对猜雷这种事情,而且一招不慎,满盘皆输。。。
简单的判断还好,有些时候还会遇到一些藏得更加隐晦的猜的时候。

扫雷判断题
假设在我们的扫雷过程中遇到了这么一个图案,确实是一件欲哭无泪的事情。不知道怎么哭的可以先把眼泪准备好,小编马上就告诉你们为啥要哭。。。从左边开始,假设第一个空位有雷,那么第二个空位没有雷,因为空位中间 1 的存在从而第三个空位有雷,依次类推。但是如果是第一个空位没有雷,而第二个空位有雷,我们也说得通。都要踩地雷了,还整个这么复杂的难题,至于么。。。
别急,后面还有更加复杂的。这里的 x 和之后的 * 号上是否有雷的情况一直相同,所以这个地雷阵就像一根传递信号的导线一样。在扫雷的地图上,我们不仅仅能够做出这种简单的传递信号的导线,其实还能够实现所有的电子电路中的逻辑门的操作。[4,5]