直接上题:
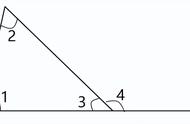
在四边形ABCD中,
AB=AD,CD=10,CB=12,
∠DAB=60°, ∠DCB=30°,
连接对角线AC,
那么AC的长度是多少?

这道题给的已知条件挺多的,又是角度,又是边长,又是两边相等,似乎应该不难,但这些条件对于求对角线的长度来说并没有什么直接的关联,所以直接求对角线有点无从下手。一般来说初中求线段长度无非就是勾股定理,相似或全等这些,在这个图形中,我们观察到两边相等且夹角为60度,那么自然可以想到这是一个等边三角形,而对角又是一个30度的角,所以是否有可能创造一个直角三角形,把对角线AC转换到这个直角三角形中就可以通过勾股定理求得了。看到60度角一般会想到旋转,如果把ABC给逆时针转60度,会发现又会产生一个新的等边三角形,而AC也会转换到一个直角三角形中,这样的思路可谓巧妙啊。
大家有什么好的想法,欢迎评论分享!
,