度的直方图
我们后面会看到,度的直方图相当重要,可用于确定我们看到的图的种类。
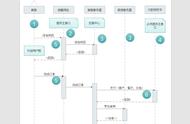
如何存储图?
你可能会好奇我们如何存储复杂的图结构?
存储图的方式有三种,取决于你想用它做什么:
- 存储为边列表:
1 2 1 3 1 4 2 3 3 4 ...
我们存储有边连接的每一对节点的 ID。
- 使用邻接矩阵,这通常是在内存中加载的方式:

邻接矩阵
对于图中的每一个可能的配对,如果两个节点有边相连,则设为 1。如果该图是无向图,则 A 是对称的。
- 使用邻接列表:
1 : [2,3, 4] 2 : [1,3] 3: [2, 4] ...
最好的表示方式取决于用法和可用的内存。图通常可存为 .txt 文件。
图可能包含一些扩展:
- 加权的边
- 节点/边上加标签
- 加上与节点/边相关的特征向量
图的类型
在这一节,我们将介绍两种主要的图类型:
- Erdos-Rényi
- Barabasi-Albert
Erdos-Rényi 模型
定义
在 Erdos-Rényi 模型中,我们构建一个带有 n 个节点的随机图模型。这个图是通过以概率 p 独立地在节点 (i,j) 对之间画边来生成的。因此,我们有两个参数:节点数量 n 和概率 p。

Erdos-Rényi 图
在 Python 中,networkx 软件包有用于生成 Erdos-Rényi 图的内置函数。
# Generate the graph n = 50 p = 0.2 G_erdos = nx.erdos_renyi_graph(n,p, seed =100) # Plot the graph plt.figure(figsize=(12,8)) nx.draw(G_erdos, node_size=10)
这会得到类似于下图的结果:

生成的图
度分布
令 pk 为随机选取的节点的度为 k 的概率。由于图构建所使用的随机方式,这种图的度的分布是二项式的: