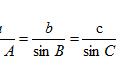我们都知道在三角形当中存在如下定理:正弦定理和余弦定理:
已知三角形ABC, 角A对应的边为a,角B对应的边为角b,角C对应的边为c,R是外接圆的半径.
正弦定理: (对边与对角的正弦函数相等)
余弦定理: (角对边的长等于相邻两边与交角存在如下公式)
接下来,我们用余弦定理来证明三角形的正弦定理:

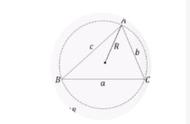
证明要用到的图
证明过程:
要证明: (如上图)
OE,OF分别垂直于AB,AC,O为三角形外接圆圆心, AO=BO=OC=R, AE=c/2,AF=b/2
AE=R*cosα AF=Rcosβ
所以: c/2=Rcosα c=2Rcosα 同理 b=2Rcosβ.............(1)
根据三角形余弦定理
将1代入得到:
整理得到:
............(2)
又因为 A=α β
根据两角和差公式: cos(α β)=cosαcosβ-sinαsinβ
代入整理得到(2)"="右边:
(2)右边=
整理得到:
又因为: 代入 整理:
(2)右边=
即:(2)右边=
又因为:sinA=sin(α β)=sinαcosβ sinβcosα
所以(2)右边= 即
因为 a/2R>0, 角A<π
所以:a/2R=sinA 同理可以证明 b/2R=sinB, c/2R=sinC
所以
a/sinA=b/sinB=c/sinC=2R
归纳: 在证明过程中我们只利用了余弦定理和三角函数正弦余弦的两角和差公式.
希望对你有所启发
,