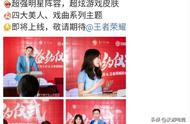
在图中的BC和BD之间进行辗转相除为什么永远不能停止。把BD减去BC,剩下一段DE。以DE为边做一个新的小正方形DEFG,那么显然DE=EF=FC(∵△EDF为等腰直角且△BEF≌△BCF)。接下来我们应该在BC和DE间辗转相除。BC就等于CD,CD减去一个DE相当于减去一个FC,就只剩下一段DF了。现在轮到DE和DF之间辗转相除,而它们是一个新的正方形的边和对角线,其比例正好与最初的BC和BD相当。于是,这个操作再次回到原问题,并且无限递归下去。最后的结论用我们的话说就是,不存在一个数x使得BC和BD的长度都是x的整倍数。于是,BD/BC不能表示为两个整数之比p/q(否则BD/p=BC/q,这就成为了那个x)。
如果说这种几何图形的证法有点晦涩难懂的话,把它“翻译”成代数证法就清楚多了:
代数解释一

于是可得p>q>c>a>…,但是,正整数必有最小元的,由此得到矛盾。
代数解释二
这种解释不过是对上述代数解法的另一种重新表述,实质上没有区别。

如图,设ABCD是边长为1的正方形,对角线AC=√2,我们用BC来量AC,在AC上截取CE=BC=1,
于是得 AC=BC AE,
即 √2=1 r1.(r1=AE<1).
第二步用AE来量BC=AB=1,即用r1来量1.注意到△ABC中BC=EC,故若过E作AC之垂线交AB于F,则FB=EF=AE=r1.在AF上截取AG=AE=r1,可见
1=2r1 r2.(r2=GF<r1).
但是,用AE来量AF,这恰巧又是用正方形的边来量它的对角线!因而GF:AE=AE:1,

这是一个永远不会结束的过程。
可以把上述过程改写成下列形式: