中考数学中关于圆的切线证明方法解读
1、首先搞清楚直线与圆的位置关系,这是学习切线的基础,关于直线与圆的位置关系判断,有下面两种方法:
(1)根据直线与圆的交点个数判断;
①直线与圆无交点,直线与圆的位置关系是相离;②直线与圆有且只有一个交点,直线与圆的位置关系是相切;③直线与圆有两个交点,直线与圆的位置关系是相交。
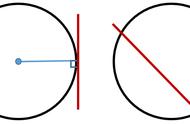
(2)根据圆心到直线的距离d与圆的半径r的大小关系判断。
①圆心到直线的距离>半径r,直线与圆的位置关系是相离;②圆心到直线的距离=半径r,直线与圆的位置关系是相切;③圆心到直线的距离<半径r,直线与圆的位置关系是相交。
2、圆中关于切线证明方法的解读:
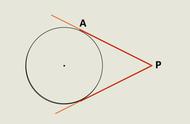
方法(1):连半径,证垂直。
具体含义:如果题目中明确告诉“切点”在圆上,那么我们就连接圆心和“切点”,去证明圆心和“切点”的连线与所证明的直线是垂直的即可。这当中要证明垂直,也就是证明角是90°,在题目已知角度的情况下可以直接求出度数,如果没告诉具体角的度数,则需要利用其他知识将角进行等量代换,间接求出角是90°。
方法 (2):作垂直,证半径。
具体含义:如果题目中并没有告诉直线与圆有一个交点,也没有标出这个点的字母,一定要注意,此时不能通过图形当中看到的情况进行解答,正确的方法是过圆心作所证直线的垂线,得到垂直90°,然后去证明作出的垂线段长度等于圆的半径即可。
最后提醒:
以上两种方法,不管哪种,在证明问题的最后总结中一定要注意对条件归纳总结,一定是“垂直 垂线段等于半径”才可以得出直线是圆的切线这一结论的。(很重要的环节,千万不可以忽略)
题目展示: