在圆这一章中,圆与直线的位置关系很重要。直线与圆有三种位置关系,分别为相离、相切与相交,尤其是相切,不仅要掌握基本定义外,还需要掌握切线的性质定理与判定定理。证明切线的方法有四种,我们需要熟练掌握两种证明切线的技巧,其中有三种思路也需要理解。

方法一:切点已知,作半径,证垂直
已知切点(该点在未确定前不能称之为切点),即当直线与圆有公共点时,选择作半径,即连接圆心与该公共点,证明垂直,常见证明垂直的思路有三种。
第一种思路:利用勾股定理的逆定理证明垂直
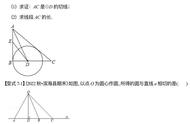
例题1:如图,AB为⊙O的直径,点P为AB延长线上一点,点C为圆⊙O上一点,PC=8,PB=4,AB=12,求证:PC是⊙O的切线.

分析:证明直线PC为圆O的切线,已知点C在圆上,即切点已知,可连接OC,证明OC⊥PC。根据已知数据可以得到PC=8,OC=6,PO=10,利用勾股定理的逆定理证明∠OCP=90°。

连接BC,OC,AC,证△PCB∽△PAC,推出∠PCB=∠A=∠ACO,∠CBA=∠OCB,根据圆周角定理求出∠ACB=∠ACO ∠OCB=90°,推出∠OCP=90°,根据切线的判定推出即可.