切线的画法以及切线的判定定理和性质定理,是学习圆的重要基础知识,我们必须理解和熟练的应用,同时还要加强我们的数学理论能力。关于这三个方面的内容,我们学习的目的是,(1)理解并掌握过一点能画出圆的切线,(2)理解并掌握经过半径的外端并且垂直于这条半径的直线是圆的切线,同时要明确切点和圆心的连线与切线垂直的性质定理。
(一)掌握切线的具体作法
同学们都知道与圆只有一个公共点的直线,或与圆心的距离等于半径的直线是圆的切线。这样通过圆外或圆上一点A就可以画出圆的切线。
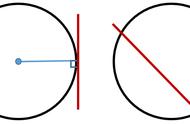
当点A在圆外时,只需要直尺画一条直线L,通过点A且与圆只有一个公共点。当点A在圆上时,只需要过点A作直线L与半径OA相垂直就可以了。说到这里,请同学们再考虑一个问题,就是过圆内的一点是否能画出圆的切线,为什么呢?
为了更加熟练的作出圆的切线,下面请同学做两个小题
1,过圆外一点A作出圆的切线
2,过圆上一点B作出圆的切线
(二)切线的判定定理
通过以上的讲述我们掌握了切线的具体作法,在作切线的过程中,就可以知道圆心O到直线L的距离等于半径r。这样的直线一定与圆相切,由此我们就可以得到一个定理,也就是切线的判定定理,即,经过半径的外端并且垂直于这条半径的直线就是圆的切线。
为了加深对切线判定定理的理解和掌握,同学们做个练习题
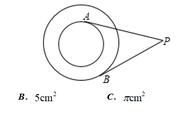
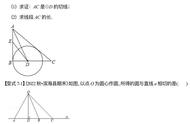
练习,已知直线AB经过圆上的点C,并且OA=OB,CA=CB,求证直线AB是⊙O的切线(图形由自己作出)
(三)切线的性质定理与推论
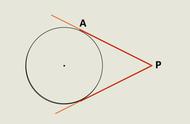
现在我们在讨论切线有什么样的性质?如果AT是圆的切线,A为切点,那么AT和半径OA是不是一定垂直呢?如果AT与OA不垂直,过O作OM丄AT,垂足为M。根据垂线段最短的性质,有OM<OA,实际上这就告诉我们圆心到直线AT的距离小于半径,于是AT就要与圆O相交,这样就与AT是圆O的切线相矛盾,因此AT与OA垂直,于是我们又得到一个新的定理,那就是切线的性质定理。即:
圆的切线垂直于经过切点的半径
因为过已知点只有一条直线与已知直线垂直,所以经过圆心垂直于切线的直线一定过切点,反过来,就可以得到过切点垂直于切线的直线也一定经过圆心,因此又得到,
推论1,经过圆心且垂直于切线的直线必经过切点
推论2,经过切点且垂直于切线的直线必经过圆心
应该注意的是在解答有关圆的切线问题时,常常需要作出过切点的半径。
还应该掌握的是圆的切线性质定理以及它的两个推论,我们知道已经涉及到的是,一条直线的三个性质(1)过圆心,(2)过切点,(3)垂直于切线。我们还可以把切线的性质定理和两个推论归纳为一个定理,即切线的综合性质定理。这个综合的切线性质定理由同学们自己去归纳。
希望同学们要带着问题1怎样画出圆的切线?2切线的判定定理是什么?3切线的性质定理是什么?我们要带着这些问题认真的阅读教材中的讲解部分,并且要认真的考虑定理的推导过程以及定理的应用。还要把教材中的例题认真的研究,思考例题是怎样应用定理去解答试题的。为了对定理的加深理解和应用,再把练习题从第一题到最后一道题全做一遍。到学校再听老师讲解,只有这样,你才能全面掌握定理的推导以及应用,才能达到学习本章节内容的目的,完成学习任务,在考场上才能有竞争的实力。
(有错误的地方,请读者和编审官帮助更改过来,谢谢!)
,