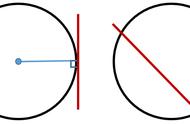
本题可借助勾股定理逆定理或者相似三角形证明垂直,再根据切线的定义进行判定。
第二种思路:利用全等证明垂直
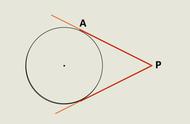
例题2:如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.求证:PB是⊙O的切线.

分析:要证明PB是切线,已知“交⊙O于点B”,即切点已知,可作半径,证垂直,即连接OB,可通过证明△POB≌△POA得到。


第三种思路:利用两个锐角互余证明垂直
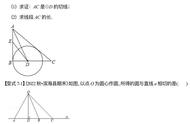
例题3:如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接DE,连接OD并延长,交BC延长线于点F.求证:DE是⊙O的切线