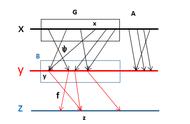
指数与对数函数图像
问题:若f(x)存在反函数,则f(x)与反函数关于直线y=x对称.
证明过程如下:
设f(x)为原函数 ,p(x,y)在原函数上, p'(x',y')在g(x)函数上, g(x)为f(x)的反函数.
根据反函数的定义:f(x)的定义域就是g(x)的值域,g(x)的定义域就是f(x)的值域,且x,y存在一一对应关系,设定f(x)存在反函数:根据定义
x'=y ..........(1)
y'=x...........(2)
计算点p与p'的中点坐标为(m,n)
则m=(x x')/2 n=(y y')/2
根据(1)(2): x x'=y y' 即:
(x x')/2= (y y')/2
所以 m=n ,无数个p与对应的p' 在直线y=x上
所以反函数与原函数关于直线y=x对称,当然前提是f(x)必须存在反函数.
- 反函数关于y=x与原函数对称的特点,可以用于一些比较大小的地方,特别是指数函数和对数函数判断大小的问题上. 就看谁在(1,1)或的上方下方.
- f(x)在y=x上方, 表示f(x)>x=y >g(x),
- f(x)在y=x下方, f(x)<x<g(x)
- f(x)与g(x)交点必然在y=x上