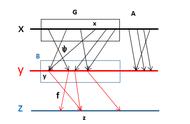
反函数的求法
一、引言
在数学中,反函数是一个非常重要的概念。
它是指对于一个函数y=f(x),存在另一个函数x=φ(y),使得对于y的每一个取值,都有x的唯一对应值。
反函数的存在性是由函数的单调性和连续性所决定的。
本文将详细介绍反函数的求法,并给出相应的例题和练习。
二、反函数的定义和性质
定义:如果对于函数y=f(x),存在一个函数x=φ(y),使得对于y的每一个取值,都有x的唯一对应值,那么称x=φ(y)为y=f(x)的反函数。
性质:
1. 反函数的定义域和值域分别是原函数的值域和定义域。
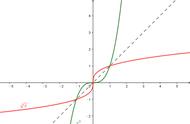
2. 反函数和原函数的关系是关于y=x对称。
3. 反函数在其定义域内是单调的。
4. 反函数的导数等于原函数导数的倒数。
三、反函数的求法
求反函数的方法主要有两种:
一种是利用反函数的定义求解,另一种是利用原函数的性质求解。
方法一:利用反函数的定义求解
步骤1:根据反函数的定义,设原函数为y=f(x),其反函数为x=φ(y)。
步骤2:将y=f(x)中的x替换为y,得到y=f(y)。
步骤3:解出y,得到x=φ(y)。
步骤4:确定反函数的定义域和值域。
例题:求函数y=2x 1的反函数。
解:将y=2x 1中的x替换为y,得到y=2y 1。
解出y,得到x=(y-1)/2,即x=φ(y)。
因此,函数y=2x 1的反函数为x=(y-1)/2。
方法二:利用原函数的性质求解
步骤1:根据原函数的性质,确定原函数的单调性和连续性。
步骤2:根据反函数的定义,确定反函数的定义域和值域。
步骤3:利用原函数的导数和单调性,求解反函数的表达式。
例题:求函数y=x^2的反函数。
解:因为函数y=x^2在x>0时单调递增,在x<0时单调递减,所以它的反函数在y>0时单调递增,在y<0时单调递减。
又因为原函数的导数为2x,所以反函数的导数为1/2√y。由此可得反函数的表达式为x=√y/2。