一、复合函数
定义:设函数 z = f ( y ) 定义在数集 B ,函数 y = ψ ( x ) 定义在数集 A ,G 是 A 中使 y = ψ ( x ) ∈ B 的 x 的非空子集 (如图1),即
G = { x ∣ x ∈ A, ψ ( x ) ∈ B } ≠ ∅ 。
对任意的 x ∈ G , 按照对应关系 ψ , 对应唯一一个 y ∈ B ,再按照对应关系 f , 对应唯一一个 z(如图1) ,即 对任意的 x ∈ G 都对应唯一一个 z 。于是在 G 上定义了一个函数 , 表为 f • ψ ,称为函数 y = ψ ( x ) 与 z = f ( y ) 的 复合函数 , 即
( f • ψ) (x) = f [ ψ ( x ) ] , x ∈ G , y 称为中间变数(如图2) 。
注:经常将函数 y = ψ ( x ) 与 z = f ( y ) 的复合函数表为 z = f [ ψ ( x ) ] , x ∈ G 。

图(1)

图(2)
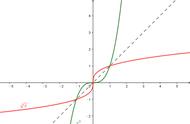
例题1、

例题1图
例题2、(三个函数生成的复合函数 )设 u = √z , z = ln y , y = 2x 3 , 则 u = √[ ln ( 2x 3 )] , x ∈ [ -1 , ∞ ] 。
二、反函数
定义:设函数 y = f ( x ) 在数集 A 有定义。
若 对任意的 x1 , x2 ∈ A ,有 x1 ≠ x2 推出 f ( x 1) ≠ f ( x 2) (或 f ( x 1) = f ( x 2) 推出 x1 = x2 ),则称函数 y = f ( x ) 在数集 A 一一对应 。
定义:设函数 y = f ( x ) 在数集 A 一一对应 ,即对任意的 y ∈ f ( A) 只有唯一一个 x ∈ A ,使 f ( x ) = y ,这是一个由 F ( A ) 到 A 的新的对应关系,称为函数 y = f ( x ) 的反函数 , 表示为