反函数图
定理1、若函数 y = f ( x ) 在数集 A 严格增加 (严格减少),则函数 y = f ( x ) 存在反函数,且反函数 x = f^(-1)( y ) 也严格增加(严格减少)。
反函数的性质:
1、单调函数必有反函数。有反函数的函数不一定是单调函数,例如反比例函数 y = K/x ( K ≠ 0 ) ;
2、奇函数不一定有反函数,例如 y = sin x , y = x - 1/x ;当奇函数存在反函数时,反函数一定是奇函数。
例如反比例函数 y = K/x ( K ≠ 0 ) 的反函数还是 y = K/x ( K ≠ 0 ) 。
3、偶函数不一定没有反函数,例如 y = 1 , x ∈ { 0 } 。
反函数与原函数的关系:
1、反函数的定义域是原函数的值域,反函数的值域是原函数的定义域;
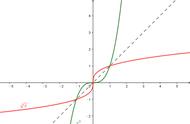
2、互为反函数的两个函数的图像关于直线 y = x 对称 ;
3、原函数若是奇函数,则其反函数为奇函数;
4、若函数是单调函数,则一定有反函数,且反函数的单调性与原函数的一致;
5、原函数与反函数的图像若有交点,则交点一定在直线 y = x 上或关于直线 y = x 对称出现 。
原函数 y = f ( x ) 与 反函数 y = f^(-1)( x ) 的图像关于直线 y = x 对称

对称图(1)
幂函数中原函数与反函数的图像关于直线 y = x 对称

(2)
指数函数和对数函数互为反函数,图像关于直线 y = x 对称

指数函数与对数函数图(1)