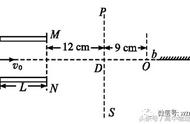
图4 实验室参考系下,线框正以速度离开磁场区域(阴影区为匀强磁场)
下面我们换到线框静止的参考系(随动系)中考察该问题。在随动系下,线框静止,没有动生电动势;磁场虽然大小和方向不随时间改变,但其存在的区域却在发生改变,因此这是一个随时间变化的磁场,会产生感生电动势。为了求解感生电动势的大小,我们首先要求解随动系下的电磁场。根据时空坐标和电磁场的参考系变换公式(公式中带撇的随动系相对不带撇的实验室系的速度为):

我们可以立即得出:在随动系下,磁场仍为匀强磁场(在黑色区域内部),磁感应强度为′=,其边界以-的速度后退;同时随动系下的电场强度不为0,而是一个与磁场存在于同一区域的匀强电场,其电场强度矢量为′=-′,其中′为随动系下′方向单位向量。这一电场就是由随动系下变化的磁场′产生的感生电场。这一感生电场绕环路的积分得到的感生电动势就是随动系下的总电动势:

有兴趣的读者可以尝试使用通量定理分别计算两个参考系中的电动势(在计算随动系中的磁通量时请注意:随动系下磁感应强度与实验室系不同,可由上文提到的电磁场参考系变换公式得到),将得到与以上相同的结果。
由此我们发现:不同参考系下的电动势是不一样的。这是由于电动势的定义是一个“等时”积分,而在相对论的闵可夫斯基时空中,不同参考系中的“同时性”不是绝对的,因此电动势不构成一个在洛伦兹变换下不变的(四维协变)标量。通过这个简单的例子,我们更加深入地理解了电动势的定义是依赖于参考系的,并且动生电动势与感生电动势紧密结合在一起:对于同一物理过程,产生的是动生还是感生电动势以及电动势的大小都与参考系的选取有关。(在低速近似下,≈1,电动势在两参考系下近似相等。)
同时,我们发现一些长期从事教学工作的同事意识里的“动生电场”其实就是从参照系变化来的,他们认为实验室参照系里的动生电动势是由洛伦兹力中×这一项贡献的,而这一项也“恰好”是随动参照系中电场′的低速近似(即把洛伦兹变换中的因子近似为1),因此称之为“动生电场”。我们认为这种说法是很不严谨的,因为在随动参照系里线圈是不动的;根据上面的讨论,在随动参照系里测到的电动势恰恰是感生电场引起的。通过洛伦兹变换改变参照系的时候,电场和磁场是要互相转换的,所以我们在讨论问题的时候必须首先搞清楚参照系,同一参照系下的物理量才可以放在一起考虑。“动生电场”的错误叫法是典型的混淆不同参照系下物理量的错误。它导致一种似乎麦克斯韦方程组里没有包括“动生电场”,似乎是不完备的错觉。更值得一提的是,《电磁场与电磁波》本科教材的修订版[第四版],将原版[第二版]正确的随动参照系电场的回路积分,错写成了实验室参照系电场的回路积分,得到了错误的法拉第定律的微分形式。事实上,麦克斯韦方程组里没有“动生电场”,因为它本来就不存在,导致动生电动势的是运动导体中的电荷在磁场下受到的洛伦兹力。
07
电磁动力学定律的完备性——场方程与洛伦兹力方程
在这篇文章的最后,笔者想要额外解释一下电磁学定律的完备性的问题。我们经常能听到一种观点:麦克斯韦用四个方程组统一了复杂的电磁现象,丰富的电磁现象完全包含在这简洁的四行方程中。抛开历史过程不谈,这一论述中的科学内容并不严谨。麦克斯韦方程组确实将大量的电磁现象总结在了一起,甚至可以从中推导出电荷守恒定律;但要想完整地描述电磁学,仅靠麦克斯韦方程组是不够的。麦克斯韦方程组是电磁场的动力学方程和约束条件,它仅描述了电荷(电流)与电磁场以及电磁场之间的局域关系。在麦克斯韦方程组中,电荷和电流是作为外部参量存在的。完备的电磁学理论一定还需要将电荷的动力学规律纳入进来——如果携带电荷的物质可以用经典力学来描述,对应的动力学规律就是洛伦兹力方程=( ×)与牛顿第二定律,如果是量子体系则是以矢势耦合到相应的薛定谔方程。在有电磁介质存在的情况下,我们通常使用麦克斯韦方程组和介质的本构关系来解决电磁学问题。实际上,介质的本构关系描述的是介质中的电荷和分子电流对于电磁场的响应,从根本上来讲是由上述携带电荷的物质场的动力学规律导出的。这一根本逻辑即使是到了用量子理论描述物质的今天也没有改变。麦克斯韦方程组加上物质的动力学规律(对于经典系统即洛伦兹力定律)就是完备的电磁动力学定律(如果这个世界上只有电磁这一种相互作用,则联立麦克斯韦方程组和描述物质的动力学方程即从原则上可求解一切物理问题)。在没有新的实验现象发现之前,这就是电动力学物理规律的“最终版本”。本文作者之一戴希教授前段时间也在知乎上表示:“任何其他版本的电磁学方程或者理论要么跟麦克斯韦方程加洛伦兹力定律在数学上严格等价,要么就是错的,没有第三种可能性。”除非有新的实验现象(例如磁单极子)被观察到,否则试图随意修改麦克斯韦场方程的一切尝试(严格的数学恒等变换除外)都将走向谬误。
附 录:
附录1:金属导电的经典模型
从经典的观点来看,导体中电子任何宏观上的定向运动都会由于晶格和晶体中的杂质对电子的散射而快速消失,从而转化为无规则的热运动。因此,想要使电子进行宏观定向运动形成电流,则一定需要外力来维持。这就是物理学中很常见的一种运动——漂移运动(drift)。有关漂移过程的物理细节我们不去过多赘述,读者只要明白基本的物理图像:在某一确定温度下,导体中的电子在无规热运动的同时,以一个确定的平均速率漂移;在室温下这个热运动速率其实很大,例如在300 K时,这一速率约为1.16×10m/s,而在弱电场下,导线中自由电子形成电流的定向移动平均速率要低多个数量级;这样,电子连续两次被散射的平均时间间隔约为其平均自由程除以热运动速率。电子在外力的作用下加速,但不会一直加速下去,因为平均时间之后,电子就会由于被散射而损失掉定向移动的速度,然后再重新开始加速;综上所述,如果我们忽略这一次一次的加速—撞击—加速—撞击的细节,电子在恒定的外力F的作用下会达到一个稳定的平均漂移速度=/,其中是电子的质量(见《费曼物理学讲义》第一卷43-3)。根据电流密度的微观表达式我们知道=,其中是电子数密度,是电子电荷量,因此,电流的大小与一个电子所受的稳定合外力(不包括撞击晶格时受到的反冲)成正比。虽然对于金属材料导电性的准确描述还是应该使用量子理论,但上述的经典模型已经能够成功地给出与实验测量结果相符的定性图像。
附录2:通量法则的证明
首先,我们需要给磁通量一个准确的定义。在数学上,一个矢量场(,)对某个有向曲面Σ的通量是一个标量,定义为该矢量场在该曲面上的“第二类曲面积分”: