初一下学期,还是以代数为主,但是几何知识也不要忽略。在几何题中,除了常考查的证明题外,也有计算题,常见的计算题有角度的计算、线段长度的计算、几何图形面积的计算。在初一下学期,学习的几何知识点主要有相交线与平行线、三角形,因此几何计算中以角度的计算为主,也会与角平分线、高线、内角和定理、外角和定理、几何图形变换之折叠变换等知识点相结合,有些题目的难度较大,可能会作为压轴题出现在考试中。

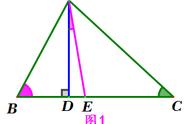
例题1:如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AD于点E,DF∥BE交AC于点F,若∠C=70°,∠BAC=58°.
(1)求∠ABE的度数;(2)求∠ADF的度数.

分析:(1)依据三角形内角和定理,即可得到∠ABC的度数,再根据角平分线的定义,即可得到∠ABE的度数;
(2)依据高线的定义,即可得出∠BED的度数,由BE∥DF,根据两直线平行,内错角相等即可得到结论。
解:(1)∵∠C=70°,∠BAC=58°,
∴∠ABC=52°,
又∵BE平分∠ABC,
∴∠ABE=∠DBE=1/2∠ABC=26°.
(2)∵AD是BC边上的高,
∴∠BED=90°-26°=64°,
又∵DF∥BE,∴∠ADF=∠BED=64°.
在直角三角形中,两个锐角互余,解题时注意有运用两直线平行,内错角相等。
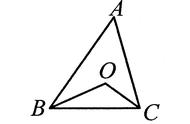
类型二:与内角和相结合例题2:如图,已知∠1=20°,∠2=25°,∠A=55°,求∠BDC的度数.

分析:根据三角形的内角和等于180°列式求出∠DBC ∠DCB,再利用三角形的内角和定理列式计算即可得解。
解:∵∠1=20°,∠2=25°,∠A=55°,
∴∠DBC ∠DCB=180°-20°-25°-55°=80°,
在△BCD中,∠BDC=180°-(∠DBC ∠DCB)=180°-80°=100°.
解本题时要注意整体思想的使用,不是每个角的度数都能直接求出,准确识图理清图中各角度之间的关系是解题的关键。