三角形中间的夹角怎么求,三角形中两边与其夹角的关系

例题3：如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE．如果∠A=α，∠CEA′=β，∠BDA'=γ，求α，β，γ三个角的之间的关系。

分析：根据三角形的外角得：∠BDA'=∠A ∠AFD，∠AFD=∠A' ∠CEA'，代入已知可得结论。

解：由折叠得：∠A=∠A'，∵∠BDA'=∠A ∠AFD，∠AFD=∠A' ∠CEA'，

∵∠A=α，∠CEA′=β，∠BDA'=γ，

∴∠BDA'=γ=α α β=2α β．

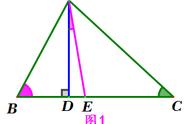
例题4：已知：如图，在△ABC中，∠ACB=90°，CD是高，AE是△ABC内部的一条线段，AE交CD于点F，交CB于点E，且∠CFE=∠CEF．求证：AE平分∠CAB．

分析：在△ADF中，利用三角形内角和定理结合对顶角相等可得出∠DAF=90°-∠AFD=90°-∠CFE，在△AEC中，利用三角形内角和定理可得出∠CAE=90°-∠CEF，再结合∠CFE=∠CEF可得出∠DAF=∠CAE，即AE平分∠CAB。

证明：∵CD⊥AB，

∴在△ADF中，∠DAF=90°-∠AFD=90°-∠CFE．

∵∠ACE=90°，

∴在△AEC中，∠CAE=90°-∠CEF．

∵∠CFE=∠CEF，

∴∠DAF=∠CAE，即AE平分∠CAB．

证明角度相等，可以利用平行线的性质，也可以利用初一上学期学习的等角（同角）的余角相等，等角（同角）的补角相等。