对于数学学习,我们强调最多的就是希望大家要好好理解和掌握数学思想方法,同时,这部分内容也是相对比较难以学习和理解。一些人从幼儿园一直到大学毕业,可能最终连什么是数学思想方法都说不出一些感受。
数学思想方法可以说是数学的灵魂和精髓,它无论在数学专业领域、数学教育范围内,还是在其它科学中,都被广为得到运用。如我们最常见的数学思想方法就就是数形结合思想,根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想,其实质是将抽象的数学语言与直观的图象结合起来,关键是代数问题与图形之间的相互转化。
在数学学习中,通过解题,我们无形中会运用到很多数学思想方法去解决问题,只是你无法通过感觉器官来感受到而已。学会运用数学思想方法,我们可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维,有助于把握数学问题的本质,这样很多问题便迎刃而解,且解法容易理解和消化。

今天我们通过多种方法来证明三角形内角和定理,使大家在一题多解中感受到数学思想方法的运用。
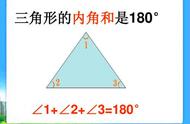
三角形内角和定理是我们最熟悉、最常用的数学基本定理之一,它是三角形的一个基本性质,也是其它定理的重要依据之一,可以说是整个几何王国的最重要的基础知识内容之一。三角形内角和定理具体内容:三角形的三个内角和等于180°。
初中数学教材安排三角形内角和定理的学习,不仅要求学生掌握好定理,更重要学会如何证明三角形内角和定理。通过证明方法的研究,使我们的学生的思维能力得到训练;通过图形的“拼凑”,培养动手能力;通过多种证明方法的学习,使学生能感受到数学思想方法的运用;通过多种证明方法的学习,让学生从不同角度去分析问题和解决问题。
三角形内角和定理证明方法一:
已知:△ABC的三个内角是∠A,∠B,∠C.求证:∠A ∠B ∠C=180°.

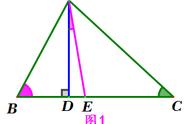
证明:过点C作CD∥BA,则∠1=∠A
∵CD∥BA
∴∠1 ∠ACB ∠B=180°
∴∠A ∠ACB ∠B=180°