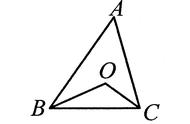
(竞赛试题)如下图所示,P是等边三角形ABC内部一点.PA=2,PB=2√3,PC=4,求△ABC的边长。

【思路点拨】要求△ABC的三边长,可猜想∠BPC=90°,不难发现由2,2√3,4构成的三角形是直角三角形.若把它们集中在一个三角形中,就可以发挥其作用了。故若把△BAP旋转到△BCM的位置,则这三条线段就集中到△PCM中,分别求出∠CPM,∠BPM即可

解:作△BCM,使BM=BP,CM=AP,则△BMC≌△BPA
∴∠MBC=∠PBA,∴∠MBP=∠CBA=60°,
∴△BPM是等边三角形,∴MP=2√3.
又∵CM=AP=2,PC=4
∴PC²=PM² CM²,且PC=2MC
∴△PCM是直角三角形,且∠CMP=90°,∠CPM=30°
又∵△PBM是等边三角形,
∴∠BPM=60°,∴∠BPC=60° 30°=90°,
∴BC²=BP² PC²=(2√3)² 4²=28,BC=2√7
故等边三角形ABC的边长为2√7.
【解后反思总结】下列情形,常实施旋转变换:
(1)图形中出现等边三角形或正方形,把旋转角分别定为60°,90°
(2)图形中有线段的中点,将图形绕中点旋转180°,构造中心对称全等三角形
(3)图形中出现有公共端点的线段,将含有相等线段的图形绕公共端点旋转两相等线段的夹角后与另一相等线段重合.
,