三角形内角和定理证明方法八:
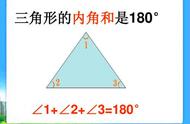
已知:△ABC的三个内角是∠A,∠B,∠C.求证:∠A ∠B ∠C=180°.

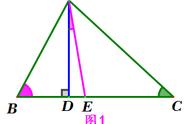
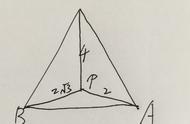
证明:若选点O在△ABC外,不在△ABC边的延长线上,则如图所示,
过点O作PQ//AC, 交BA、BC的延长线分别于P、Q,
再过点O作 EO//BC, DO//AB ,即得:
∠EOP=∠Q=∠C, ∠EOD=∠ODC=∠B,
∠DOQ=∠APO=∠BAC,
∵∠DOQ ∠EOD ∠EOP =180°,
∴∠ACB ∠B ∠BAC=180°.

从上面这八种三角形内角和定理证明方法当中,我们发现要想证明三角形的三个内角之和等于180°,就需要把问题转化到平角的大小为180°。因此,在解决问题的过程中,我们就想方设法将三角形的三个内角“转化成”一个平角,如利用添加辅助线的方法构造出一个平角,再运用一定技巧"移动"内角,将其构造成一个平角,这就是数学当中化归转化思想方法的运用。
通过三角形内角和定理的证明,我们可以很清楚感受到数形结合、化归转化等数学思想方法的运用。只要大家认真专研解题方法,多总结反思,慢慢就学会数学思想方法的运用。如在平时数学学习过程中,学会从不同角度去分析解决问题,我们的思维能力就会得到锻炼,不仅掌握好了基础知识内容,更学会运用方法和技巧去解决实际问题,最终掌握数学思想方法,提高数学素养。
因此,基于数学思想方法的重要性,因此《数学课程标准》将数学思想方法列为数学目标之一。
,