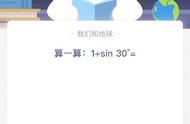
在头条上看到一个数学题(一家长辅导孩子做题,发到头条上):
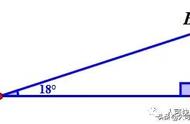
题目:如图所示,在△ABC中,∠A=30°,∠CDB=45°,点D是AC的中点,求∠C的度数?

这道题不是很难,但也不简单,我下面给出三种解答:

方法一:如图,过点C作CE⊥AB,垂足E在AB上,连接DE.因为∠A=30°,CE⊥AB,点D为AC中点, 易知△CDE为等边三角形,所以∠CDE=∠DCE=60°, 因为∠BDC=45°, 所以∠BDE=60°-45°=15°,又 ∠ABD=∠BDC-∠BAC=45°-30°=15° =∠BDE, 所以△BDE是等腰三角形, 则CE=DE=BE, 则△BCE是等腰直角三角形, 有∠BCE=45°, 所以∠C=∠BCE ∠DCE=45 60°=105°.