“B事件发生的条件下,A事件发生的概率”?
"在A集合内有多少B的样本点"?
“在B约束条件下,A发生的概率变化为?”
“B事件中的一个样本点,同时也落在A样本点集合的概率是多少”
“将B作为样本空间,则A的概率变为多少”
1.条件概率在古典概率中到底该怎么被定义?
2.从交事件AB来推导条件概率公式
3.在考研古典概率中,条件概率公式的一些不足
4.在现实生活中如何理解条件概率?
一、条件概率在古典概率中到底该怎么被定义?
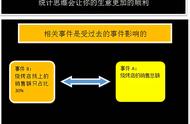
我们经常把条件概率定义为“B事件发生的条件下,A事件发生的概率”,这个定义如果一开始就扔出来,往往会对后面的学习产生误导。
因为B事件发生可以看作是“随机事件B中的一个基本样本点的发生”,但是古典概率中样本点都是平等的,所以是不可能互相产生影响的。也就是说事件B中的一个基本样本点,就古典概率来讲,对A事件中包含的任意样本点都不会产生关系。
这个推论可以总结为“古典概率的所有样本点之间都是等概率的,都是平等的”
其实这就是古典概率的两条定义之一,那到底在古典概率中,应该怎么定义条件概率呢?
其实应该定义为
“B随机事件中包含的任意一个样本点,也同时属于A事件的样本点集合的概率”

那为什么要这样定义呢,还是需要从交事件P(AB)的计算中来推导。
二.从交事件AB来推导条件概率公式
交事件的意思就是“A、B同时发生的概率”,如果我们知道P(A)和P(B)那么如何计算P(AB)呢?
许多人都想到直接相乘:

但是P(AB)真的一定等于P(A)乘P(B)吗?
这里其实隐藏了一个条件就是:事件A和事件B两者没有任何关系,只有这样才能直接相乘。
但是古典概率的各个样本点之间的关系是
“古典概率各个样本点事件互为互斥事件”
这意味着什么呢?意味着发生了事件A中的一个样本点,则事件A集合之外的样本点一定会不会发生。
这也就是说如果事件A,B存在于一个样本空间,那么从古典概率的角度来看,它们之间就是一定存在联系的,不能这样直接乘。
那应该怎么做呢?我们还是从V-N图的思路来想,P(AB)可以看作是从样本空间任意选取一个样本点,正好落在AB的重复交合区域的概率。

*那么我们已经知道P(A)的概率了,也就是“在空间中任意选取一个点,落在A的概率”,如果我们把范围再缩小一次,也就是说我们可以得知,在A集合内有多少B的样本点,这样一个比例,然后用P(A)去乘这个比例,就可以得到最终结果P(AB)。