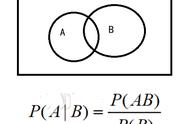条件概率的推导过程是怎么样的,为什么那么定义?
条件概率的定义并没有特别的推导过程,而是直观地从概率的定义和集合论的概念中得出的。
首先,我们需要理解概率的基本定义。在统计学中,某个事件发生的概率通常被定义为这个事件发生的次数与实验重复的次数之比。例如,如果我们掷一个公正的六面骰子,每个面出现的概率都是1/6,因为每次投掷,每个面出现一次的次数与总的投掷次数的比值在大量重复试验后趋近于1/6。
然后,我们再引入集合论的概念。我们可以把每次试验的所有可能结果看作是一个样本空间(即全集),每个事件(比如投掷骰子得到一个特定的点数)则是样本空间的一个子集。于是,概率可以被理解为一个事件所包含的元素数量占样本空间元素总数的比例。
如果我们想要考虑的是条件概率,即给定某个事件B已经发生的情况下,另一个事件A发生的概率,那么我们实际上是在缩小了的样本空间(即事件B所包含的元素)中考虑事件A。于是,事件A在事件B发生的条件下发生的概率,

,被定义为事件A与事件B的交集(即既属于A又属于B的元素)在事件B中的比例,或者写作:
这个定义直观地反映了条件概率的概念:给定事件B已经发生,我们的样本空间缩小为事件B,我们关注的是这个新样本空间中也属于事件A的元素所占的比例。
,