二、举个形象的例子
上面的讲得有点抽象,举个例子:
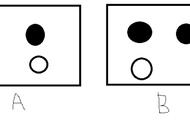
假设:小学⼀年级有共100⼈,其中有男⽣生30⼈。穿⽩袜⼦的⼈数共有20个,这20个人里面有5个是男⽣。

1. 男生的概率 P(男生)= 男生数/总人数 = 30/100;
2. 穿白袜的概率 P(白袜) = 穿白袜人数/总人数 = 20/100 ;
如果我们只研究穿白袜的男生的概率,我们会以下三个不同的视角:

A:以30个男生作为总体样本,P(白袜|男生)= 穿白袜男生数/男生数=5/30;
B:以20个穿白袜的学生作为总体样本,P(男生|白袜)=穿白袜男生数/穿白袜学生=5/20;
C:以一年级学生作为总体样本,P(白袜∩男生)= 穿白袜的男生数/总人数 = 5/100;
因为穿白袜子的男生始终还是那5个人,只是总体样本不同导致的分母不同,
如果要让三个数值相等那么“参考系”就要保持统一。我们选取一年级全体学生作为总体样本。如下图:

假设我们不知道C的计算结果,我们从视角A或者视角B,重新推导在一年级总体样本中,“找出”穿白袜的概率: