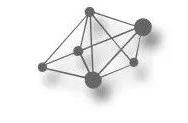
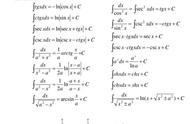的椭圆曲线,不可能是模曲线,也就是说谷山---志村猜想将不成立。这被称为“弗雷命题”。
也就是说如果费马大定理成立的话,那么就会是模曲线,谷山—志村猜想也将成立。
弗雷命题在数学史的意义非凡,显然,费雷命题和谷山-志村猜想是相矛盾的,有谷山-志村猜想错误的情况下,上述椭圆曲线才会存在。如果能同时证明这两个命题, 根据反证法就可以知道费马大定理不成立这一假定是错的, 从而就证明了费马大定理。
也就是说一旦费雷命题得证,费马大定理就与谷山---志村猜想等价。或者说得更直接些:谷山-志村猜想一旦成立,那么费马大定理必将成立。
而在1986年美国加州大学伯克利分的肯.里贝特教授完成了弗雷命题的证明,并当即在这届国际数学家大会内外传开。世界数学界为之兴奋。
自此,费马大定理就与谷山---志村猜想等价。只要证明了谷山—志村猜想,那么就可以证明费马大定理。
怀尔斯用200页证明摘取费马大定理这颗明珠1986年,英国数学家安德鲁·怀尔斯 听到里贝特证明弗雷命题后,感到攻克费马大定理到了最后攻关阶段,并且这刚好是他的研究领域,他开始放弃所有其它活动,躲在自己家的阁楼里开始最后的攻坚阶段。
整整7年的时间,在历经无数次碰壁之后,在历经常人无法想象的困难之后,1993年6月,英国剑桥大学举行了一次注定载入史册数学会议。

安德鲁·怀尔斯做了一系列报告,标题晦涩难懂——“模形式、椭圆曲线、伽罗瓦表示”。他的论证过程冗长且技巧性很强,到第三次演讲进行20分钟后才进入尾声。为了强调所得结果,他在最后打上了:
费马大定理,是数学史上的著名猜想,由 17 世纪法国律师兼业余数学家皮耶·德·费马提出,但经过350年仍然没有完备的证明。普林斯顿大学的教授怀尔斯躲在家中的阁楼里,默默研究这个古老难题整整七年。现在,他要在会场公布自己的证明。

这段话直接震撼了整个数学家,低调的怀尔斯一时之间名声大噪,然而证明不是你说证明了就行了的啊,古往今来,多少数学家都说自己证明了,结果被纷纷打脸,其中还包括柯西、拉梅这样的大数学家。
所以怀尔斯向世界顶级数学期刊Inventiones Mathematicae提交了长达200页的证明。该期刊的编辑随后将这份手稿分发给6位审稿人,这项工作没有一个审稿人想接,因为这会让这些审稿人非常痛苦,因为他们压根无法进行推演,而且很多地方他们压根无法理解,任何一个步骤有所错漏,都将导致整个论证的倾覆。
他们每个人都仔细检查了自己所负责部分的每个逻辑环节。而这其中有许多他们无法理解的论证,他们只能给怀尔斯发邮件,而怀尔斯会回复澄清问题,将每一个微小步骤进行细致地说明,这些编审就会在进行推导求证。

从六月份提交证明,一直到8月底,审核都没有结束,而在这个时候,其中一位审稿人普林斯顿大学的数学家Nick KatzKatz和他的法国同事Luc Illusie在这个时候发现了问题,
怀尔斯对一个问题的解释并不能说服这两位审稿人,因为他们无论如何进行推导求证都感觉其中存在问题。在进一步研究后,怀尔斯明白Katz找到了论文数学逻辑框架中的一个缺陷。起初,简单的修复看似可行。但当怀尔斯着手修复缺陷时,逻辑框架的碎片开始脱落。
这就好像一个拼好的乐高一样,一旦一块积木消失,那么整个乐高将随之崩塌。怀尔斯这个时候慌了。他无法忍受自己花费7年时间摘下的明珠拱手让给他人。
到1993年12月,距剑桥演讲已经过去了6个月, 怀尔斯还是没有办法找到这块遗失的积木,他好不容易拼成的乐高在他身后正摇摇欲坠。