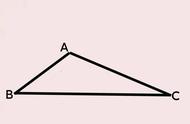
如图,直角三角形的两条直角边长分别是a、b(单位:厘米),斜边长为c。

三角形面积=c×高=a×b,
“c×高=a×b”两边同时“×2”得:
c×高=a×b
根据“一个乘数=积÷另一个乘数”得:
高=(a×b)÷c=
即:直角三角形斜边上的高=两条直角边的积÷斜边
例 如图,直角三角形的三边长分别是3厘米、4厘米、5厘米,沿斜边旋转一周得到一个立体图形,这个立体图形的体积是多少?

解析
(1) 这个立体图形可以看成是两个圆锥组合而成,两个圆锥底面半径都是CD。
(2) 直角三角形斜边上高CD=(厘米),所以半径长为厘米。
(3) 立体图形的体积=AC为高的圆锥体积+BC为高的圆锥体积
=π××AC×+π××BC×
=π××(AC+BC) ×
=π××5×
……
答案
(厘米)
π××5×
=π×××5×
=π(立方厘米)
答:这个立体图形的体积是π立方厘米。
练习
1. 已知直角三角形的三边长分别是5厘米、12厘米、13厘米,这个直角三角形斜边上的高是( )厘米。
2. 如图,直角三角形的三边长分别是6厘米、8厘米、10厘米,沿斜边旋转一周得到一个立体图形,这个立体图形的体积是多少?


1.
解析
直角三角形斜边上的高=两条直角边的积÷斜边
(厘米)
答案
2.
解析
(1) 这个立体图形可以看成是两个圆锥组合而成,两个圆锥底面半径都是CD。
(2) 直角三角形斜边上高CD=(厘米),所以半径长为厘米。
(3) 立体图形的体积=AC为高的圆锥体积+BC为高的圆锥体积
=π××AC× +π××BC×
=π××(AC+BC) ×
=π××10×
……
答案
(厘米)
π××10×
=π×××10×
=π(立方厘米)
答:这个立体图形的体积是π立方厘米。
,