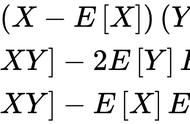【问题导入】相关分析中研究两事物之间的线性相关性是通过计算相关系数等方式实现的,并通过数值的大小来判断事物之间线性关系的强弱。但对于一个较复杂的变量而言,其影响因素是多方面的。仅仅利用线性相关系数来表示两事物间的关系往往存在夸大的趋势。例如:在对学生的体能调查中,研究学生的体能素质与运动量之间的关系时,体能素质还受自身身高、父母体重等因素影响。此时单纯利用相关系数来评价变量间的相关性就有失偏颇,有必要在剔除其他相关因素影响的条件下计算变量间的相关。如何在SPSS中控制其他变量的影响下分析两变量之间的相关关系将是重点。
偏相关分析原理
核心概念
偏相关分析:也称为净相关分析,它在控制其他变量的线性影响的条件下分析两变量间的线性相关,利用偏相关系数(净相关系数)来描述其关系。
偏相关系数:控制变量个数为1时,偏相关系数称为一阶偏相关;控制两个变量时,偏相关系数称为二阶偏相关;控制零个变量时,偏相关系数称为零阶偏相关系数也就是相关系数。在分析x和y之间的净相关时,当控制了x2的线性作用后,x1和y之间的一阶偏相关定义为:


原理解析
SPSS中的偏相关分析需要两个步骤:第一,计算样本偏相关系数;第二,通过假设检验对两样本来自的两总体是否存在显著的偏相关进行推断。
1.计算偏相关系数
利用样本数据计算总体间的偏相关系数,反映两变量间的净相关程度强弱。偏相关系数的取值范围及大小含义与相关系数相同,在此不再赘述。
2.推断两总体是否存在显著的净相关
检验偏相关分析显著性的主要操作步骤如下:
(1)提出零假设H:两总体的偏相关系数与零无显著差异。
(2)选择检验统计量:对应不同的相关系数选择不同的检验统计量。(3)计算检验统计量的观测值和对应的概率p值。
(4)显著性决策:根据给定的显著性水平α值(0.05),若概率p值小于α值应拒绝零假设,认为两总体不是零相关。反之概率p值若大于α值,则不能拒绝零假设,可认为两总体零相关。
案例解析:分析在控制经济增长率的影响下分析教育投资与学生增长率之间的关系
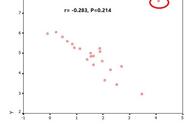
【案例呈现】在前面的“教育投资"案例中我们可以看到教育投资与学生增长率之间存在着较强的相关性,但在控制经济增率的影响下,教育投资与学生增长率之间是否还存在相关性呢?我们用偏相关分析来进行推断。

【操作步骤】