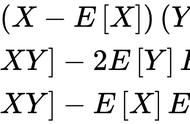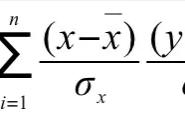01
Pearson相关系数的问题
虽然看起来,Pearson相关系数简直是完美无瑕了!其实不然,Pearson相关系数也存在一些问题。
首先,Pearson相关系数的前提条件是要两个变量满足近似正态分布。这要求在计算相关系数前,要作正态性检验。而且,多数情况下变量不一定满足正态分布的,这就无法使用Pearson相关系数。
其次,Pearson相关系数是在方差和协方差的基础上得到的,对离群值比较敏感。如下图所示的散点图,除右上角一个离群值外,其余数据点呈明显的线性相关关系,但真实计算出来的Pearson相关系数r=-0.283,P=0.214,显然Pearson相关系数无法正确衡量X和Y的线性相关性。

所以,为了解决这几个问题,后来数据科学家们又定义了其它几种相关系数公式。
02
相关系数种类
常用的相关系数主要有三种:Pearson相关系数、Spearman秩相关系数和Kendall τ相关系数。

03
Pearson相关系数

04
Spearman秩相关系数
Spearman Rank相关系数,即斯皮尔曼秩相关系数(Spearman Rank Order Correlation Coefficient,简称SROCC),是英国心理学家、统计学家斯皮尔曼根据积差相关的概念推导而来的。
在Peaarson相关系数中,所有的数据都要参与公式计算,特别是离群值的存在,导致相关系数的计算不准确。为了避免离群值的影响,在Spearman等级相关系数公式中,并不是采用原始的数据对(xi,yi)来计算,而是利用数据的秩对(Ui,Vi)来定义相关系数。将Pearson相关系数的计算公式中的x和y用相应的秩代替即可得到Spearman相关系数,其公式如下: