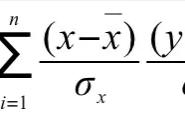随机变量的期望和方差反映的是随机变量自身的一维分布特征。然而一维特征之外,随机变量之间可能存在着种种相关关系。比如人的身高与体重,气象的温度与湿度,商品的广告费用与销量等等。有没有数字特征来反映变量间的这种二维关系呢?下面我们就来谈谈描述随机变量之间相关关系的数字特征。
一、标准化1.1标准化的过程我们知道两个变量的协方差就是一个二维数字特征:

但协方差的取值受两个变量各自的量纲影响,数字的意义并不明显,我们只知道独立的随机变量,协方差为零,其他的关系呢?无法从协方差的数字中直接读出。
今天我们将提出一种方法,对协方差进行无量纲化的修正。会有什么样的结果呢?
我们采用的方法就是对变量进行标准化处理。
如果随机变量X的方差DX存在,且DX>0,则称
X*= (X-EX)/√DX为X的标准化随机变量。我们看到标准化处理就是对原随机变量减其期望再除上其根方差。
由期望方差的运算性质我们可得:
EX*=0
D X*=1
数值如此简单,难怪X*被称为标准化变量。
通过标准化处理任意的随机变量,都转换成了期望为零,方差为1的标准化变量。
标准化的目的就是消除量纲希望以及方差的不同,对数据比较所造成的影响。
1.2标准分的应用在综合评价中,标准分就是一个重要指标。
例如某次考试后,语文和数学的成绩都为均值80的正态分布。

但语文的方差为9,数学的方差为4;甲同学语文80分,数学86分。乙同学数学80分,语文86分。
从总分来看,两人总分相同。请问你觉得他们的能力是否也相同呢?两个86分,由正态分布的3σ原则,数学的86分是不是更加不易?是不是较语文的86分含金量更高?如何体现这种差异呢?对了,标准化处理。
我们分别计算两个86分对应的标准化成绩。
y^*=(86-80)/3=2;
x^*=(86-80)/2=3
减期望再除上根方差,数学的标准分就比语文的标准分高,而单纯的总分没能体现出这样的差别。
所以标准化的思想在综合评价中,特别是分布差异较大的指标时,是一个重要的处理方案。
二、相关系数2.1相关系数的取值既然随机变量标准化后,消除了量纲上的差异。那标准化变量X*与Y*的协方差就是两个变量二维特征的本质体现。
我们称X*与Y*的协方差为原变量X 与Y 的相关系数。
即为ρ(X,Y)=cov(X*,Y*)。
由协方差的运算性质:

那相关系数能不能较好的反映随机变量x 与y 之间的关系呢?我们来研究一下相关系数的性质。
相关系数的取值在-1到1之间。
证明:
令X*= (X-EX)/√DX,Y*= (Y-EY)/√DY,则
由于X*与Y*都是标准化变量,方差为1,协方差即为相关系数ρ(X,Y)。
由于方差总是大于等于0的,所以解不等式有2ρ(X,Y)≥-1;
同理由差的方差公式:
解不等式2ρ(X,Y)≤1。
从这个性质之相关系数取值以零为中心,左右对称,以±1为界。
2.2相关系数的含义那相关系数取不同的值都代表了什么意思呢?
ρ(X,Y)等于±1的充要条件为X与Y 以概率为1完全线性相关。
即 Y与X有线性的函数关系:
证明:
从刚才性质一的证明过程之相关系数等于1时,等价于D(X*-Y*)=0
而方差为零的变量将以概率1取值于他的期望。
由于X*与Y*为标准化变量,所以X*-Y*的期望为零,即以概率1有X*-Y*等于零。
P{ X*-Y*=0}=1即X*=Y*
P((X-EX)/√DX=(Y-EY)/√DY)=1,即=(X-EX)/√DX = (Y-EY)/√DY
同理,当ρ(X,Y)等于-1时。等价的有P{ X*=-Y*}=1。
表明ρ(X,Y)绝对值等于1时,X 与Y 具有最大的线性相关关系。
ρ(X,Y)=1时:
Y可以表示为X 的斜率为正的线性函数。
ρ(X,Y)=-1时:
Y 可以表示为X 的斜率为负的线性函数。
ρ(X,Y)=0时,表示X 与Y 没有一点儿线性相关的关系,称为X 与Y不线性相关。
ρ(X,Y) 不等于零时,表示X 与Y有部分的线性相关性,称X 与Y线性相关。其中,若大于零为正相关若小于零为负相关。ρ(X,Y)的绝对值的大小反映了相关性程度的大小。如越接近于1。表示Y 越接近于X 的正系数的线性表达;如越接近于-1表示Y越接近于Y 的负系数的线性表达。若越接近于零,表示Y 与X 的线性表达程度越来越弱,直到完全没有线性关系。

X与Y·1 独立则协方差为零,从而相关系数也为零。所以独立则不相关,反之则不然。虽然X与Y不相关,不具有线性关系,但可能存在非线性的关联,那就不是独立的了,所以独立与不相关,并不等价。
但正态分布是一个特例,独立与不相关是等价的。
对于二维正态随机变量
(X、Y)~N(μ1,μ2,σ12,σ22,ρ),其中中的参数ρ,可以证明它就是X、Y 的相关系数。
由二维正态分布的性质。X、Y独立的重要条件是ρ等于零,即X、Y不相关。