什么情况下用最大公约数,最大公约数什么意思举例

在数学中，最大公约数（Greatest Common Divisor，简称GCD）是两个或多个整数的公共因数中最大的一个。求解最大公约数在数学和实际问题中都具有重要意义。本文将详细讲解最大公约数的求解方法，包括几种常用的算法和应用。

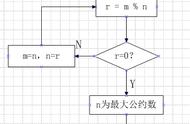
辗转相除法，又称欧几里德算法，是一种常用且高效的求解最大公约数的方法。该算法基于一个原理：两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数。

具体步骤如下：

1. 用较大数除以较小数，得到余数。
2. 将较小数作为被除数，余数作为除数，再次进行相除。
3. 重复上述步骤，直到余数为0。
4. 此时，除数即为最大公约数。

更相减损术也是一种古老的求解最大公约数的方法。它通过反复用两个整数中较大的数减去较小的数，直到两个数相等为止，最终得到的相等的数即为最大公约数。

然而，更相减损术的效率较低，尤其是当两个数较大时，可能需要较多次的减法操作。

辗转相减法是辗转相除法的一种变体。它利用较大数减去较小数，得到一个新的差值，然后再用较小数减去这个差值，重复进行，直到两个数相等。最终得到的相等的数即为最大公约数。

与更相减损术相比，辗转相减法减少了大量的减法操作，提高了效率。

质因数分解法是另一种常用的求解最大公约数的方法。它将两个数分别进行质因数分解，然后找出它们的公共质因数，最终将这些公共质因数相乘得到最大公约数。

最大公约数在数学中有广泛的应用，例如：

• 简化分数：可以将分子分母同时除以它们的最大公约数，得到最简分数。
• 求解最小公倍数：利用最大公约数和两个数的乘积等于它们的最小公倍数。
• 确定比例关系：最大公约数可以帮助我们找到两个数之间的最简比例关系。

最大公约数作为一个基本的数学概念，在数学运算和实际问题中都具有重要的意义。通过不同的求解方法，我们可以高效地找到两个或多个数的最大公约数，从而在各种情况下都能够得到准确的答案。

（注：具体数值示例和计算过程请参考相关数学教材或在线数学工具。）