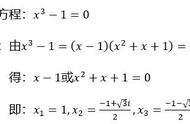这其实就是用弦图推导出了求根公式,把a=8,b=12代入公式可得x₁=2,x₂=6。

到了宋代又出现了解二次方程的巧妙方法——四因积步法,或者称为杨辉方法。

杨辉方法来源于赵爽弦图。公元1275年南宋数学家杨辉所著《田亩比类乘除捷法》书中,引用了公元1078年前后北宋数学家刘益所著《议古根源》一书中讨论的一个题目,大意是一块长方形的田面积为864平方步,已知宽比长少12步,问长和宽是多少步?
杨辉在书中解题时画了一个弦图。

显然,长方形的长加宽等于大正方形的边长。求出大正方形的面积再开平方就可以得到长方形的长宽之和了。
即(a b)²=(a-b)² 4ab......(1)
=12² 4×864
=144 3456
=3600
显然,长方形的长宽之和为60,已知长宽之差为12,再用小学数学的和差问题公式计算就得到长=36,宽=24。
杨辉方法相当于解二次方程x(x-12)=864。题目的步是古代的长度单位,一步等于五尺。
杨辉方法的代数意义就是恒等式(1)。
杨辉方法求出了方程的一个正根,能否求出另外一个根呢?
我们来解方程x(x-12)=864
令a=x,b=x-12,则a b=2x-12,a-b=12,ab=864,把数据代入恒等式(1),得
(2x-12)²=12² 4×864=3600=60²
两边开平方,得
2x-12=±60
这样就实现了一元二次方程的降次。
解方程得,x₁=36,x₂=-24。
所以,我们可以根据杨辉方法的代数意义,不画图也可以求出方程的两个根。
再用杨辉方法解李永乐的例题。
x²-8x 12=0
原方程化为
x(x-8)=-12
令a=x,b=x-8,则a b=2x-8,a-b=8,ab=-12,把数据代入恒等式(1),得
(2x-8)²=8² 4×(-12)=16=4²
两边开平方,得
2x-8=±4
解之得
x₁=6,x₂=2
方程的复数解李永乐在视频里指出,即使判别式小于零,韦达定理也是成立的。
我们可以举个例子来验证一下。
例题2
x²-4x 20=0
用求根公式计算可得
x₁=2 4i,x₂=2-4i
两根之和满足韦达定理,再看两根之积:
(2 4i)(2-4i)=4-(4i)²
=4-(-16)
=20
还是满足韦达定理。
当然,初中数学不研究复数,知道方程没有实数根就可以了。