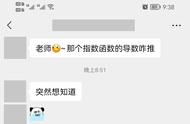
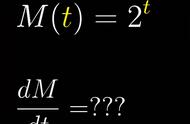基本初等函数的求导公式表
例如:
原函数为:y=x^3 3x^2 7x 9;一阶导数为:y=3x^2 6x 7;二阶导数为:y=6x 6;(即y=3x^2 6x 7的导数)三阶导数为:y=6。(即y=6x 6的导数)
在物理定义上,如果我们设原函数为位移(s),一阶导数为速度(v),二阶导数为加速为(a)。这些都是我们熟知的,但是位移的三阶导数有许多人甚至听都没听说过。
位移的三阶导数为:急动度,也叫做力变率,即加速度随时间的变化率。
更让人意外的是,急动度定义的出现,不是因为物理学,而是因为生物学。在生活中人们总会遇到一些不舒心的场景,但仅凭速度和加速度已经无法解释这些现象,更别谈解决问题了,此时,急动度就被挖掘出来了。
举个栗子,当轿车速度突然发生剧烈变化时,加速度会突然改变,此时,轿车就具有了急动度,乘客会感到不舒服,甚至是受伤也都是因为急动度在作怪。
为了保证良好的乘坐体验,汽车工程师们把急动度作为评判乘客不舒适程度的指标。(具有恒定加速度和零急动度的人体,感觉最舒适)总之,你可以测量位置、看见速度、感觉加速度、厌恶急动度。
其实,除了三阶导数之外还有四阶导数(痉挛度),甚至更高阶...
通过上面的例子我们可以得出一个结论:高阶导数可以看作是对上一级导数的修正(后者控制前者的变化趋势)。
通货膨胀又是什么?
通货膨胀(inflation):指在货币流通条件下,因货币供给大于货币实际需求,也即现实购买力大于产出供给,导致货币贬值,而引起的一段时间内物价持续而普遍地上涨现象。其实质是社会总需求大于社会总供给 (供远小于求)。

还有一种不是很严谨的理解:钱印多了。
三阶导数为何会被用来解决通货膨胀问题?
为了方便理解,超模君直接举了个栗子
假设在 a 年与 b 年之间的某个国家的消费价格指数(CPI)由函数 f(t) 表示,(a≤t≤b),那么 f'(t) 描述了消费价格指数的变化率,俗称通货膨胀率(f'(t)>0表示物价将上涨,f'(t)<0表示物价将下降)。而 f''(t)表示了通货膨胀率的变化率,f'''(t)则表示了通货膨胀率变化率的变化率。
在经济领域,一个看似极微小的事情,都极有可能造成整个系统的分崩离析。(蝴蝶效应)此时,选择一种更精准、细致的解决方案就显得尤其重要。
通过 f'''(t) 对 f''(t) 进行修正, f''(t) 再对 f'(t) 进行修正,其实质就是通过“三阶导数”更精准把控通货膨胀率,从而遏制通货膨胀过热的趋势。
虽然尼克松在任期间没有彻底的解决美国的滞胀危机,但却为美国的新经济政策作了理论基础,也因此成为了第一个通过“三阶导数”来推进连任活动的美国总统。
三阶导数还被用来解决房价问题
其实,“三阶导数”的应用在生活中也是无处不在。人们最关注的房价控制问题也运用了“三阶导数”。

若设房价为原函数,则一阶导数为:房价上涨率;
房价涨幅不高于人均收入增长(GDP)的10%,则一阶导数为常数了。
二阶导数为:房价上涨率的变化率;
遏制部分城市房价上涨过快,则二阶导数为常数了。
三阶导数为:房价上涨率的变化率的变化率。
遏制了房价上涨过快的趋势,则三阶导数为常数了。
相信很快就需要动用“四阶导数”了。
甚至还能用来解决一些婚姻问题

此时,就会有模友们说,“幸好我还是单身。”
热心肠的超模君肯定不能眼睁睁地看着大家天天吃“狗粮”呀。
但在解决“单身问题”上,三阶导数(高阶导数)就显得有些鸡肋,因为导致单身的原因有点多,求导根本导不过来...
“超级数学建模”(微信号supermodeling),每天学一点小知识,轻松了解各种思维,做个好玩的理性派。60万数学精英都在关注!
,