抽丝剥茧,详细解析初中数学题386
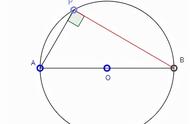
386:如图所示,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C。
⑴求证:CB∥PD
⑵若BC=3,sin∠P=3/5,求⊙O的直径。

解析:1.证明CB∥PD很简单,
∵∠P=∠C,∠1=∠C,
∴∠P=∠1,
∴CB∥PD(内错角相等)。
2.因为有已知条件sin∠P=3/5,
而∠P=∠BCE,
所以sin∠BCE=3/5;
又因为直径AB⊥CB,
再把AC连接起来,
就将问题放在Rt△ACB中去进行了,
如下图所示,

∵∠BCE=∠CAB,
∴sin∠CAB=3/5,
又BC=3,
∴AB=BC/sin∠CAB
=3/3/5=5。
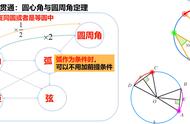
小结:圆周角定理及其理论
1.圆周角定理:圆上—条弧所对的圆周角等于它所对的圆心角的一半。
2.推论:
①同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
②直径所对的圆周角是直角;
90°的圆周角所对的弦是直径。
,