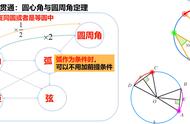
为什么圆内接三角形的一边若是直径,该边的对角是90度?

现在用几何证明角APB=90度。

这是内接角的一个已知且非常有用的性质,它们是同一条弧对着的圆心角的一半,或者是同一弦对着的圆心角的一半。当弦是直径时,圆心角是2直角和对应的圆周角都是直角。
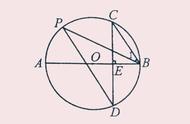
设P是直径为AB、圆心为O的圆上的一点,即OA = OB = OP,表示同一圆的三个半径。这使得三角形成为AOP和BOP等腰
其中,底角相等,它们的和等于一个外角:
∠OAP ∠APO =∠BOP
同样
∠OBP ∠BPO =∠AOP
但由于∠OAP =∠APO
且∠OBP =∠BPO,则有
2∠APO =∠BOP
同样
2∠BPO =∠AOP
把两者相加
2∠APO 2∠BPO =∠AOP ∠BOP=180°。
换句话说,
∠APB =∠APO ∠BPO = 90°。
证法2:利用同弧的圆周角等于圆心角的一半的这个定理,可知AB是圆心角所在的弧为180度,因此其圆周角APB=90度。
,