先来看一下这节一开始的思考题。

截取自人教版《高中物理》
虽然小汽车和火车的速度都是从0达到100km/h,但是二者所用的时间不同,火车用的时间更多一些。用“速度大”或者“速度变化大”无法描述这种情况,因为这里并没有涉及时间,所以我们引入一个新的物理量——加速度
小汽车和火车的速度都在增加,或者说两者都在做变速运动,并且它们的“速度变化”相同,速度都是从0达到100km/h,但所用的时间不同,汽车用了10s,火车用了300s。这两种情形的本质区别是“速度变化的快慢”不同。
看来“速度变化的快慢”是一个不同于“速度”的概念。两个物体速度变化相同,所用时间短的速度变化得快,所用时间长的速度变化得慢。如果两个物体速度变化不同,所用时间也不同,怎样比较它们速度变化的快慢呢?
在前面学习速度时,位移表示的是位置的变化。要比较位置变化的快慢,可以用位移除以时间。同理,要比较速度变化的快慢,可以用速度的变化量除以时间。
物理学中把速度的变化量与发生这一变化所用时间之比,叫作加速度(acceleration)。通常用a 表示。若用Δv 表示速度在时间Δt 内的变化量,则有,表示物体的初速度,表示物体的末速度。
加速度虽然有“速度”二字,但它不是一种速度。在国际单位制中,加速度的单位是米每二次方秒,符号是或 。加速度反映的是物体速度变化得快慢,所以也称作速度随时间的变化率(简称速度的变化率)。
在加速度的定义式中,速度的变化量是一个矢量,时间是一个标量,它们的比值加速度仍然是一个矢量,加速度的方向是与速度变化量的方向相同的。
我们用加速度描述物体的运动,并不是指物体一定要加速。在直线运动中,速度增加,说明加速度的方向与速度的方向一致;速度减小,说明加速度的方向与速度的方向相反。
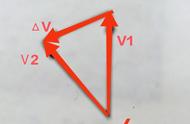
如下图,汽车原来的速度是,经过一小段时间Δt 之后,速度变为。为了在图中表示加速度,我们以原来的速度的箭头端为起点,以后来的速度的箭头端为终点,作出一个新的有向线段,它就表示速度的变化量Δv。由于加速度,所以加速度a的方向与速度的变化量Δv的方向相同。确定了Δv的方向,也就确定了加速度a 的方向。

再看一个例子,如下图甲,当物体从静止开始沿着斜面下滑,速度越来越大,做加速运动,加速度方向与速度方向相同;图乙中,物体以一定的初速度从地面开始沿斜面向上运动,速度会越来越小,也许还没到达顶端速度就减小为零了,做减速运动,加速度方向与初速度方向相反。

如果在一段时间内,物体做直线运动,而且加速度方向一直保持不变,就叫做匀变速直线运动。
如果在直线运动中,物体的加速度为零,物体做什么运动?很明显物体的速度一直不变,在做匀速直线运动。
具体计算加速度的时候,一定要注意初速度和末速度的方向。
例如,一个足球以8m/s的速度飞来,足球运动员迎球一脚,将足球以12m/s的速度踢回。已知作用时间为0.2s,求足球的加速度。
可以直接用加速度公式计算,但是一定要注意方向,所以需要规定正方向,将矢量式转化为标量式进行计算。
取足球原来的运动方向为正方向,那么初速度,末速度
根据公式带入数据加速度
结果中的负号表示足球的加速度方向与初速度方向相反。
总结
加速度是描述物体速度变化快慢的物理量,是物体速度变化量与这个变化量所用时间的比值,即,是一个矢量。加速度的方向与速度变化的方向相同。
,