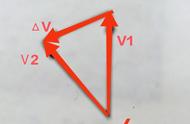
牛顿第二定律不仅适用于单个物体,同样也适用于系统,系统内各物体的加速度可以相同也可以不相同.当系统内各物体加速度相同时,系统看成一个整体(或看成一个质点)分析其受到的外力及运动情况,利用牛顿第二定律列出方程F=(m₁+m₂)a.
若系统内各物体加速度不相同,如m₁、m₂的加速度分别为a₁、a₂,这时可利用牛顿第二定律列出方程F=ma₁+m₂a₂.该方程又称牛顿第二定律的分立式,注意F是系统受到的合外力,并注意方程的矢量性,亦即F、a₁、a₂必须在同一直线上,并根据其方向确定其正负.

系统内物体的加速度不同,也可用整体法来研究处理,若一个系统内各物体的加速度不相同,而又不需要求系统内物体间的相互作用力时,对系统列式F=m₁a₁+m₂a₂较简便,因为对系统分析外力,可减少未知的内力,使列式方便,大大简化了运算.用此种方法要抓住三点:
(1)分析系统受到的外力;
(2)分析系统内各物体的加速度大小和方向;
(3)建立直角坐标系,分别在两个方向上对系统列出方程.
例题:如图甲所示,斜面体b的质量为M,放在粗糙的水平地面上.质量为m的滑块a以一定的初速度沿粗糙的斜面向上滑,然后又返回,此过程中b没有相对地面移动.

由此可知()
A.地面对b一直有向右的摩擦力
B.地面对b一直有向左的摩擦力
C.地面对b的摩擦力方向先向左后向右
D.地面对b的支持力一直小于(M+m)g
例题:倾角θ=37°、质量M=5kg的粗糙斜面位于水平地面上,质量m=2kg的木块置于斜面顶端,从静止开始匀加速下滑,经t=2s到达底端,运动路程L=4m,在此过程中斜面保持静止(sin37°=0.6,cos37°=0.8,g取10m/s²),

求:(1)地面对斜面的摩擦力大小与方向;
(2)地面对斜面的支持力大小。