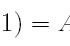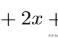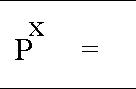霍尔维茨判据:探索实系数多项式根与稳定性的奥秘
霍尔维茨判据,这个看似复杂但极具深度的数学概念,为我们提供了一种判断实系数多项式根是否为负实数的有效方法。这个判据不仅在纯数学领域具有重要地位,更在控制理论和稳定性分析中发挥着不可替代的作用。

霍尔维茨判据的核心在于多项式系数的符号交替出现以及其主子式值均大于零这两个条件。这两个条件共同构成了判断多项式根是否为负实数的充要条件。当多项式的系数满足符号交替的条件时,我们可以初步判断其可能具有负实数根。而主子式值均大于零的要求,则进一步确保了多项式的所有根均为负实数。
这个判据之所以重要,是因为它在控制理论和稳定性分析中扮演着至关重要的角色。在控制系统中,我们往往需要判断一个系统的稳定性,即系统是否能够在受到扰动后恢复到原来的状态。霍尔维茨判据为我们提供了一种判断系统稳定性的有效方法。通过计算系统特征多项式的系数和主子式,我们可以利用霍尔维茨判据判断系统的所有根是否为负实数,从而判断系统的稳定性。
霍尔维茨判据的应用不仅仅局限于控制系统稳定性分析,它还广泛应用于各种实际问题中。例如,在电路分析中,我们可以通过霍尔维茨判据判断电路的稳定性;在信号处理中,我们可以利用该判据分析滤波器的性能;在经济学中,我们甚至可以用它来分析经济模型的稳定性。
值得一提的是,霍尔维茨判据的提出不仅丰富了数学理论,更为我们提供了一种深入理解系统稳定性的工具。通过霍尔维茨判据,我们可以更直观地把握系统的动态特性,为系统设计和优化提供有力的支持。
当然,霍尔维茨判据并不是万能的。在实际应用中,我们还需要结合其他数学工具和方法,如劳斯判据、根轨迹法等,来综合分析系统的稳定性。同时,我们也需要关注霍尔维茨判据的局限性和适用范围,避免在实际应用中出现错误或误导。
总之,霍尔维茨判据作为数学和工程领域的一项重要工具,为我们提供了一种判断实系数多项式根是否为负实数的有效方法。它在控制理论和稳定性分析中的应用,不仅有助于我们深入理解系统的动态特性,更为我们提供了一种优化系统设计和提高系统性能的有力手段。
,