今天给大家讲一篇关于统计学的知识,虽然当前机器学习,深度学习等大数据技术火得一塌糊涂,但归根结底,离不开统计学的基础,而谈到统计学,假设检验几乎是提到的最多的词语,到底什么是假设检验, 什么是P值,什么时候用t检验,什么时候用F检验,非统计学背景的同学可能一脸懵逼,接下来我就讲下什么是假设检验

首先明确下假设检验在统计学里的地位:统计推断是统计学的重要分支,做统计推断有两个重要方法,即参数估计与假设检验。参数估计是用样本统计量估计总体参数,简单来说就是样本表现啥样,我就推断总体是啥样。而假设检验,则顾名思义,先提出一个假设,然后检验假设是否靠得住,例如假设均值为μ,然后根据样本信息检验均值是不是μ,通常我们是要去证明均值不是μ,也就是去推翻原假设。逻辑上采用的是反证法,根据统计上的小概率原理,即假设是这样,但样本表现却不是这样,从而否定原假设。
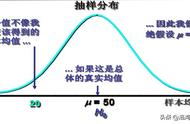
举例来说,某官方数据说居民人均收入10000,但我觉得这个不对,于是就局部范围内做了个统计(假如样本有代表性),统计出来平均值为7000, 那我这个结果有没有信服力,那我们可以检验一下,计算出P值为0.0002,那我可以很自信地说官方数据不对,不值得信。因为P值为0.0002意味着,如果居民人均工资为1w, 那么我统计出均值为7k的概率为0.0002,这么小的概率竟然这么容易就让我选的这个局部统计碰上了,显然真实的人均工资不可能为1w啊, 这就是根据小概率原理来推翻原假设。
假设检验的基本步骤接下来我们讲一下假设检验的步骤,讲述过程中你也许会有疑问,为什么这样,不要担心,先往下看,我会陆续对假设检验的细节作出补充,如果未涉及到可以在评论中提出,我会补充上):

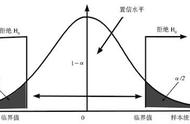
步骤1,提出假设,也就是我猜结果会是什么。猜完之后进入步骤2,即我要拿什么去验证假设,这里我们叫做检验统计量。检验没有绝对的对错,所以我们要设定一个显著性水平,就是步骤3,相当于设定一个门槛,在门外面就拒绝进门,统计学上叫拒绝域,拒绝的是原假设。套路第四步就是将门在哪儿计算出来,依据的是前两步确定的检验统计量以及显著性水平。最后就可以做出决策啦,看一下到底在门里面还是门外面。
接下来将提到的步骤跟大家详细说一下:假设的提出包括原假设与备择假设。原假设(H0)则是我们收集证据想要推翻的假设, 而备择假设(H1)则是要去支持的,所以大家可以根据实际情况来设定原假设与备择假设。原假设与备择假设互斥。假设检验是围绕着对原假设是否成立展开的。假设检验还会涉及到两类错误的问题,这个内容较多,会单独讲解。
检验统计量是用于假设检验决策的统计量。如何去选择统计量呢?这与参数估计相同,需要考虑样本总体个数,样本大小,通常大于30个样品我们认为是大样本,以及总体方差是否已知,如果未知,可以用样品方差近似计算。是不是感觉有些头晕,撑住,这是做假设检验的关键,告诉你什么情况下采用什么样的检验方法,记住这儿,以后就不会没心没肺的只会t检验啦。贴心的我给大家整理了检验统计量的选择图谱,对家直接对号入座就可以啦,记住这些,再遇到假设检验的问题,你会感觉厉(niu)害(bi)的不要不要的。

配对样本的检验:两个总体参数的假设检验过程中,我们假定样本是独立的,但有种情况下样本间可能存在相依的关系,这种情况下两个正态总体的问题可以按照一个样品总体进行分析。举个例子:我想测试某个洗涤产品的洗涤效果,我可以测一下衣服洗之前的洁净程度,用产品洗之后的洁净程度,这样就得到了两个总体,可以按照方差未知的小样本t检验进行分析。但是,同是一件衣服,洗之前和洗之后数据之间是有对应关系的,我可以将洗前洗后的洁净程度做差值,检验差值是否为0,这样就转化为一个总体样本的t检验。
具体的统计量的计算公式此处未给出,主要考虑到现在都用统计软件进行计算,关键要明确自己的统计问题,选择恰当的检验统计量,然后在统计软件上就可以开挂了!