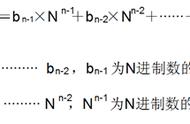相信有很多很多人都知道二进制,八进制,十进制,十六进制,那你知道这些进制都有什么作用呢?以及个禁止之间是怎么转换的呢?那么今天我就来说说什么是二进制,什么是八进制,什么是十进制,什么是十六进制以及他们之间是怎么转换的,
十进制转二进制
进制表

二进制
对于整数部分,用被除数反复除以2,除第一次外,每次除以2均取前一次商的整数部分作被除数并依次记下每次的余数。另外,所得到的商的最后一位余数是所求二进制数的最高位。
对于小数部分,采用连续乘以基数2,并依次取出的整数部分,直至结果的小数部分为0为止。故该法称“乘基取整法”。
给你一个十进制,比如:6,如果将它转换成二进制数呢?
10进制数转换成二进制数,这是一个连续除以2的过程:
把要转换的数,除以2,得到商和余数,
将商继续除以2,直到商为0。最后将所有余数倒序排列,得到数就是转换结果。
听起来有些糊涂?结合例子来说明。比如要转换6为二进制数。
“把要转换的数,除以2,得到商和余数”。
二进制转十进制二进制数转换为十进制数
二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……
所以,设有一个二进制数:0110 0100,转换为10进制为:
下面是竖式:
0110 0100 换算成十进制
第0位 0 * 20 = 0
第1位 0 * 21 = 0
第2位 1 * 22 = 4
第3位 0 * 23 = 0
第4位 0 * 24 = 0
第5位 1 * 25 = 32
第6位 1 * 26 = 64
第7位 0 * 27 = 0
公式:第N位2(N)
100
用横式计算为:
0 * 20 0 * 21 1 * 22 0 * 23 0 * 24 1 * 25 1* 26 0 * 27 = 100
0乘以多少都是0,所以我们也可以直接跳过值为0的位:
1 * 22 1 * 25 1*26 = 100
十进制转八进制10进制数转换成8进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成8。
来看一个例子,如何将十进制数120转换成八进制数。
用表格表示:
被除数
计算过程
商
余数
120
120/8
15
0
15
15/8
1
7
1
1/8
0
1
120转换为8进制,结果为:170。
八进制转十进制八进制就是逢8进1。
八进制数采用 0~7这八数来表达一个数。
八进制数第0位的权值为8的0次方,第1位权值为8的1次方,第2位权值为8的2次方……
所以,设有一个八进制数:1507,转换为十进制为:
用竖式表示:
1507换算成十进制。
第0位 7 * 80 = 7
第1位 0 * 81 = 0
第2位 5 * 82 = 320
第3位 1 * 83 = 512
--------------------------
839
同样,我们也可以用横式直接计算:
7 * 80 0 * 81 5 * 82 1 * 83 = 839
结果是,八进制数 1507 转换成十进制数为 839
十进制转十六进制10进制数转换成16进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成16。
同样是120,转换成16进制则为:
被除数
计算过程
商
余数
120
120/16
7
8
7
7/16
0
7
120转换为16进制,结果为:78。
十六进制转十进制16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。字母不区分大小写。
十六进制数的第0位的权值为16的0次方,第1位的权值为16的1次方,第2位的权值为16的2次方……
所以,在第N(N从0开始)位上,如果是是数 X (X 大于等于0,并且X小于等于 15,即:F)表示的大小为 X * 16的N次方。
假设有一个十六进数 2AF5, 那么如何换算成10进制呢?
用竖式计算:
2AF5换算成10进制:
第0位: 5 * 160 = 5
第1位: F * 161 = 240
第2位: A * 162 = 2560
第3位: 2 * 163 = 8192
-------------------------------------
10997
直接计算就是:
5 * 160 F * 161 A * 162 2 * 163 = 10997
(别忘了,在上面的计算中,A表示10,而F表示15)
现在可以看出,所有进制换算成10进制,关键在于各自的权值不同。
假设有人问你,十进数 1234 为什么是 一千二百三十四?你尽可以给他这么一个算式:
1234 = 1 * 103 2 * 102 3 * 101 4 * 100
二进制转八进制(11001.101)(二)
整数部分: 从后往前每三位一组,缺位处用0填补,然后按十进制方法进行转化, 则有:
001=1
011=3
然后我们将结果按从下往上的顺序书写就是:31,那么这个31就是二进制11001的八进制形式
八进制转二进制整数部分:从后往前每一位按十进制转化方式转化为三位二进制数,缺位处用0补充 则有:
1---->1---->001
3---->11
然后我们将结果按从下往上的顺序书写就是:11001,那么这个11001就是八进制31的二进制形式
二进制转十六进制二进制和十六进制的互相转换比较重要。不过这二者的转换却不用计算,每个C,C 程序员都能做到看见二进制数,直接就能转换为十六进制数,反之亦然。
我们也一样,只要学完这一小节,就能做到。
首先我们来看一个二进制数:1111,它是多少呢?
你可能还要这样计算:1 * 20 1 * 21 1 * 22 1 * 23 = 1 * 1 1 * 2 1 * 4 1 * 8 = 15。
然而,由于1111才4位,所以我们必须直接记住它每一位的权值,并且是从高位往低位记,:8、4、2、1。即,最高位的权值为23 = 8,然后依次是 22 = 4,21=2, 20 = 1。
记住8421,对于任意一个4位的二进制数,我们都可以很快算出它对应的10进制值。
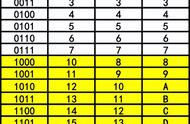
下面列出四位二进制数xxxx 所有可能的值(中间略过部分)
仅四位的二进制数
快速计算方法
十进制值
十六进制值
1111
8 4 2 1
15
F
1110
8 4 2 0
14
E
1101
8 4 0 1
13
D
1100
8 4 0 0
12
C
1011
8 0 2 1
11
B
1010
8 0 2 0
10
A
1001
8 0 0 1
9
9
……
0001
0 0 0 1
1
1
0000
0 0 0 0
0
0
二进制数要转换为十六进制,就是以4位一段,分别转换为十六进制。
如:
二进制数
1111 1101
1010 0101
1001 1011
对应的十六进制数
FD
A5
9B
十六进制转二进制反过来,当我们看到 FD时,如何迅速将它转换为二进制数呢?
先转换F:
看到F,我们需知道它是15(可能你还不熟悉A~F这六个数),然后15如何用8421凑呢?应该是8 4 2 1,所以四位全为1 :1111。
接着转换 D:
看到D,知道它是13,13如何用8421凑呢?应该是:8 4 1,即:1101。
所以,FD转换为二进制数,为: 1111 1101
由于十六进制转换成二进制相当直接,所以,我们需要将一个十进制数转换成2进制数时,也可以先转换成16进制,然后再转换成2进制。
比如,十进制数 1234转换成二制数,如果要一直除以2,直接得到2进制数,需要计算较多次数。所以我们可以先除以16,得到16进制数:
被除数
计算过程
商
余数
1234
1234/16
77
2
77
77/16
4
13(D)
4
4/16
0
4
结果16进制为: 0x4D2
然后我们可直接写出0x4D2的二进制形式: 0100 1101 0010。
其中对映关系为:
0100 -- 4
1101 -- D
0010 -- 2
同样,如果一个二进制数很长,我们需要将它转换成10进制数时,除了前面学过的方法是,我们还可以先将这个二进制转换成16进制,然后再转换为10进制。
下面举例一个int类型的二进制数:
01101101 11100101 10101111 00011011
我们按四位一组转换为16进制: 6D E5 AF 1B
再转换为10进制:6*167 D*166 E*165 5*164 A*163 F*162 1*161 B*160=1,843,769,115
二进制,八进制,十进制,十六进制有什么作用呢?这些进制都有什么作用呢?在我们生活中有很多电器都用到了数字电路,比如电脑就是用的这些进制进行运算才使得计算机有这么多的功能
,